Cho Sn = 5/(1.2.3) + 8/(2.3.4) +.....+ (3n +2) / n(n + 1)(n + 2). Chứng minh rằng S2008 < 2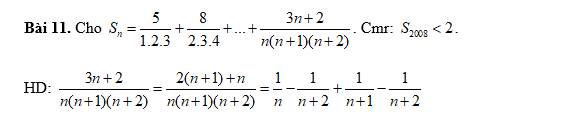 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
0
DA
0
DM
0
24 tháng 9 2021
4A = 4.[1.2.3 + 2.3.4 + 3.4.5 + … + (n – 1).n.(n + 1)]
4A = 1.2.3.4 + 2.3.4.4 + 3.4.5.4 + … + (n – 1).n.(n + 1).4
4A = 1.2.3.4 + 2.3.4.(5 – 1) + 3.4.5.(6 – 2) + … + (n – 1).n.(n + 1).[(n + 2) – (n – 2)]
4A = 1.2.3.4 + 2.3.4.5 – 1.2.3.4 + 3.4.5.6 – 2.3.4.5 + … + (n – 1).n(n + 1).(n + 2) – (n – 2).(n – 1).n.(n + 1)
4A = (n – 1).n(n + 1).(n + 2)
A = (n – 1).n(n + 1).(n + 2) : 4.
6 tháng 1 2018
\(N=1.2.3+2.3.4+...+n\left(n+1\right)\left(n+2\right)\)
\(4N=1.2.3.4+2.3.4.4+...+4n\left(n+1\right)\left(n+2\right)\)
\(4N=1.2.3.4+2.3.4.\left(5-1\right)+....+n\left(n+1\right)\left(n+2\right)\left[\left(n+3\right)-\left(n-1\right)\right]\)
\(4N=1.2.3.4+2.3.4.5-1.2.3.4+...+n\left(n+1\right)\left(n+2\right)\left(n+3\right)-\left(n-1\right)n\left(n+1\right)\left(n+2\right)\)
\(4N=n\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
\(4N+1=n\left(n+1\right)\left(n+2\right)\left(n+3\right)+1\)
\(=n\left(n+3\right)\left(n+1\right)\left(n+2\right)+1\)
\(=\left(n^2+3n\right)\left(n^2+2n+n+2\right)+1\)
\(=\left(n^2+3n\right)\left(n^2+3n+2\right)+1\)
\(=\left(n^2+3n+1-1\right)\left(n^2+3n+1+1\right)+1\)
\(=\left(n^2+3n+1\right)^2-1+1=\left(n^2+3n+1\right)^2=t^2\)(1 số bất kì thỏa mãn)
Vậy \(4N+1\) là số chính phương (đpcm)