Giải phương trình nghiệm nguyên sau:
6.(6x2 + 3y2 + z2) = 5t2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)

\(\Leftrightarrow x^2+3xy+3y^2+xy-2x-6y=5\)
\(\Leftrightarrow x\left(x+3y\right)+y\left(x+3y\right)-2\left(x+3y\right)=5\)
\(\Leftrightarrow\left(x+y-2\right)\left(x+3y\right)=5\)
Bảng giá trị:
| x+y-2 | -5 | -1 | 1 | 5 |
| x+3y | -1 | -5 | 5 | 1 |
| x | -4 | 4 | 2 | 10 |
| y | 1 | -3 | 1 | -3 |
Vậy \(\left(x;y\right)=\left(-4;1\right);\left(4;-3\right);\left(2;1\right);\left(10;-3\right)\)

6x2-3xy+17x-4y+5=0
⇔ -3xy-4y=-6x2-17x-5
⇔ 3xy+4y=6x2+17x+5
⇔ y(3x+4)=6x2+17x+5
6x2+17x+5 ⋮ 3x-4 vì x, y ∈ Z
⇔ 6x2+17x+12-7 ⋮ 3x+4
⇔ 6x2+8x+9x+12-7 ⋮ 3x+4
⇔ 2x(3x+4)+3(3x+4)-7 ⋮ 3x+4
=> 7 ⋮ 3x+4
=> 3x+4 ∈ Ư(7)={-1,1,-7,7}
3x+4=1 ⇔ x=-1 (lấy)
3x+4=-1 ⇔ x=\(\dfrac{-5}{3}\) (loại)
3x+4=-7 ⇔ x=\(\dfrac{-11}{3}\)(loại)
3x+4=7 ⇔ x=1 (lấy)
thay vào tính thì y={-6,4} (bạn tự làm nhá)
vậy (x,y)={(-1,1),(-6,4)}


Phương trình bậc hai 6x2 + x + 5 = 0
Có a = 6; b = 1; c = 5; Δ = b2 – 4ac = 12 – 4.5.6 = -119 < 0
Vậy phương trình vô nghiệm.

Phương trình bậc hai 6x2 + x – 5 = 0
Có a = 6; b = 1; c = -5; Δ = b2 – 4ac = 12 – 4.6.(-5) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
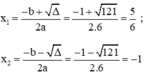
Vậy phương trình có hai nghiệm là -1 và 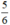

a) Phương trình bậc hai
2 x 2 – 7 x + 3 = 0
Có: a = 2; b = -7; c = 3;
Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 2 . 3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
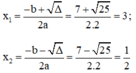
Vậy phương trình có hai nghiệm là 3 và 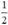
b) Phương trình bậc hai 6 x 2 + x + 5 = 0
Có a = 6; b = 1; c = 5;
Δ = b 2 – 4 a c = 12 – 4 . 5 . 6 = - 119 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 6 x 2 + x – 5 = 0
Có a = 6; b = 1; c = -5;
Δ = b 2 – 4 a c = 12 – 4 . 6 . ( - 5 ) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
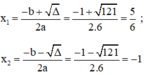
Vậy phương trình có hai nghiệm là -1 và 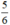
d) Phương trình bậc hai 3 x 2 + 5 x + 2 = 0
Có a = 3; b = 5; c = 2;
Δ = b 2 – 4 a c = 5 2 – 4 . 3 . 2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
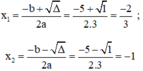
Vậy phương trình có hai nghiệm là -1 và 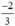
e) Phương trình bậc hai y 2 – 8 y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b 2 – 4 a c = ( - 8 ) 2 – 4 . 1 . 16 = 0 .
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
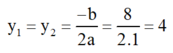
Vậy phương trình có nghiệm kép y = 4.
f) Phương trình bậc hai 16 z 2 + 24 z + 9 = 0
Có a = 16; b = 24; c = 9; Δ = b 2 – 4 a c = 24 2 – 4 . 16 . 9 = 0
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:
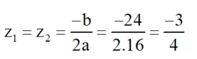
Vậy phương trình có nghiệm kép 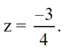
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 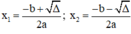
+ Nếu Δ = 0, phương trình có nghiệm kép 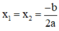 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

a) Thay x = -1 vào VT và VP của PT ta được VT = -2 và VP = 1. Vì VT ≠ VP nên x = -1 không là nghiệm của PT đã cho.
b) Tương tự, vì VT = VP = -2 nên t = -1 là nghiệm của PT đã cho.

\(x^4+y^4=3y^2+1\Leftrightarrow-y^4+3y^2+1=x^4\ge0\)
\(\Rightarrow-y^4+3y^2+1\ge0\Rightarrow\frac{3-\sqrt{13}}{2}\le y^2\le\frac{3+\sqrt{13}}{2}\)
Mà \(y\in Z\Rightarrow y^2\)là số chính phương \(\Rightarrow y^2=0;1\)
*\(y^2=0\Rightarrow x^4=1\Rightarrow x=-1;1\)
*\(y^2=1\Rightarrow x^4+1=3+1\Rightarrow x^4=3\Rightarrow x\notin Z\)
Vậy phương trình có nghiệm nguyên \(\left(-1;0\right),\left(1;0\right)\)