Tứ giác ABCD có BC=CD và DB là tia phân giác của góc D.Chứng minh rằng ABCD là hình thang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

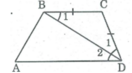
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.
⇒ ∠ B 1 = ∠ D 1 (tính chất tam giác cân)
Mà ∠ D 1 = ∠ D 2 ( Vì DB là tia phân giác của góc D)
Suy ra: ∠ B 1 = ∠ D 2
Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)
Vậy ABCD là hình thang.

ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang

Ta có hình vẽ: A B C D 1 1 2
Ta có: BC= CD (gt)
=> \(\Delta BCD\) cân tại C
=> góc B1 = góc D1
mà góc D1 = D2 (gt)
=> góc D2 = góc B1
mặt khác 2 góc D2 và B1 đang ở vị trí so le trong
=> AB // CD
=> tứ giác ABCD là hình thang

B C D A
Vì BC=CD=>Tam giác BCD cân tại C=>\(\widehat{CBD}=\widehat{CDB}\)(1)
Vì DB là tia phân giác của góc D => \(\widehat{CDB}=\widehat{ADB}\)(2)
Từ (1) và (2) => \(\widehat{CBD}=\widehat{ADB}\),mà 2 góc ở vị trí so le trong
=> AD song song với BC.
=> ABCD là hình thang.

Chú ý tam giác CBD cân tại C. Khi đó cùng với DB là phân giác góc S ta chứng minh được A D B ^ = C B D ^
CB=CD
=>góc CBD=góc CDB
mà góc ADB=góc CDB
nên góc CBD=góc ADB
=>AD//BC
=>ABCD là hình thang