A B C D F E 40độ 50độ a) Tính góc ACD b) Tính góc DCE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
25 tháng 10 2023
a) Do AB//HD \(\Rightarrow\widehat{BAC}=\widehat{ACH}\) (2 góc so le trong)
\(\Rightarrow\widehat{ACH}=40^o\)
b) Do HD//EG \(\Rightarrow\widehat{HCE}=\widehat{CEG}\) (2 góc so le trong)
\(\widehat{HCE}=50^o\)
Mà: \(\widehat{ACE}=\widehat{ACH}+\widehat{HCE}\)
\(\Rightarrow\widehat{ACE}=40^o+50^o=90^o\)
LD
4 tháng 6 2017
Hình bạn tự vẽ.
Xét \(\Delta ABC\)cân tại A ta có:
\(\widehat{DAC}=180^o-2\widehat{ACD}\)
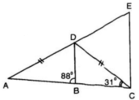
\(\widehat{DAC}=180^o-2\cdot31^o=118^o\)
Mà \(\widehat{DAC}=\widehat{ABD}+\widehat{ADB}\)( góc ngoài tại đỉnh A của \(\Delta ABD\))
Nên \(118^o=88^o+\widehat{ADB}\)
\(\Rightarrow\)\(\widehat{ADB}=118^o-88^o=30^o\)
Mặt khác \(\widehat{ADB}=\widehat{DEC}\)( 2 góc so le trong và BD // EC )
\(\Rightarrow\)\(\widehat{DEC}=30^o\)
Ta có:
\(\widehat{ACE}=\widehat{ABD}\)( 2 góc so le trong và BD // EC )
\(\widehat{ABD}=88^o\left(gt\right)\)
\(\Rightarrow\)\(\widehat{ACE}=88^o\)
Mà \(\widehat{DCE}=\widehat{ACD}+\widehat{ACE}\)
Nên \(\widehat{DCE}=31^o+88^o=119^o\)
Ta có:
\(\widehat{ACD}=\widehat{ADC}\)( \(\Delta ACD\)cân tại A)
\(\widehat{ACD}=31^o\)
\(\Rightarrow\)\(\widehat{ADC}=31^o\)
Xét \(\Delta ECD\)ta có:
\(\widehat{DCE}>\widehat{EDC}>\widehat{DEC}\left(119^o>31^o>30^o\right)\)
\(\Rightarrow\)\(ED>EC>CD\)( Quan hệ cạnh góc đối diện trong tam giác )
Vậy cạnh \(DE\)lớn nhất trong \(\Delta CDE\)
29 tháng 7 2023
6: bậc là 7
5: A
4: A
2B
1B
3:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔABD=ΔEBD
b: ΔBAD=ΔBED
=>BA=BE
=>ΔBAE cân tại B
mà góc ABE=60 độ
nên ΔBAE đều
29 tháng 11 2016
cho tam giác ABC có góc A = 90 độ .kẻ AH vuông góc với BC (H thuộc BC). trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BD=AH .chứng minh rằng
a/ tam giác AHB=tam giác DBH
b/ AB//DH
c/ tính góc ACB. biết góc BAH=35 độ