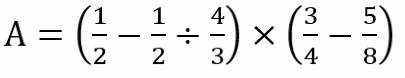
Mik cần gấp !!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Xét ΔABC có
M là trung điểm của bC
I là trung điểm của AC
Do đó: MI là đường trung bình của ΔABC
Suy ra: MI=AB/2=3(cm)

Ta có: \(\left\{{}\begin{matrix}\left(x+5\right)^2\ge0\forall x\\\left|x-y+1\right|\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(x+5\right)^2+\left|x-y+1\right|\ge0\forall x,y\)
\(\Rightarrow-\left[\left(x+5\right)^2+\left|x-y+1\right|\right]\le0\forall x,y\)
\(\Rightarrow-\left(x+5\right)^2-\left|x-y+1\right|\le0\forall x,y\)
\(\Rightarrow P=-\left(x+5\right)^2-\left|x-y+1\right|+2018\le2018\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x+5=0\\x-y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-5\\y=x+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-4\end{matrix}\right.\)
Vậy \(Max_P=2018\) khi \(x=-5;y=-4\).
$Toru$


\(\dfrac{-1}{9}.\dfrac{-3}{5}+\dfrac{5}{-6}.\dfrac{-3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\\=\dfrac{1}{9}.\dfrac{3}{5}+\dfrac{5}{6}.\dfrac{3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\\ =\dfrac{3}{5}\left(\dfrac{1}{9}+\dfrac{5}{6}-\dfrac{7}{2}\right)\\ =\dfrac{3}{5}.\dfrac{-23}{9}\\ =-\dfrac{23}{15}\)

\(a,\dfrac{35\times36\times14\times3}{6\times50\times7\times9}=\dfrac{7}{10}\)





 Giúp mik với, mik đang cần gấp ạ!!!
Giúp mik với, mik đang cần gấp ạ!!!
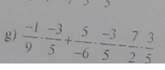
 giúp mik với ạ mik cần gấp chiều thi huhu
giúp mik với ạ mik cần gấp chiều thi huhu
A=( \(\dfrac{1}{2}-\dfrac{1}{2}:\dfrac{4}{3}\) ) x ( \(\dfrac{3}{4}-\dfrac{5}{8}\) )
A= ( \(\dfrac{1}{2}-\dfrac{1}{2}\times\dfrac{3}{4}\) ) x \(\dfrac{1}{8}\)
A = (\(\dfrac{1}{2}-\dfrac{3}{8}\) ) x \(\dfrac{1}{8}\)
A= \(\dfrac{1}{8}\) x \(\dfrac{1}{8}\)
A = \(\dfrac{1}{64}\)
A= 1/64