chứng minh rằng nếu a.d=b.c thì a b/a = c d/c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(\frac{a}{b}<\frac{c}{d}\)
\(\Rightarrow\frac{ad}{bd}<\frac{bc}{bd}\)
\(\)\(\Rightarrow\) ad < bc
đúng nha !!!
Để a/b , a+c/b+d thi a(b+d)< b (a+c)<=> ab+ad < ab +bc <=>ab < bc <=> a/b < c/d
Để a+c/b+d < c/d thì (a+c).đ < (b+d).c <=> ab+cd < bc + cd <=> ad < bc <=> a/b < c/d

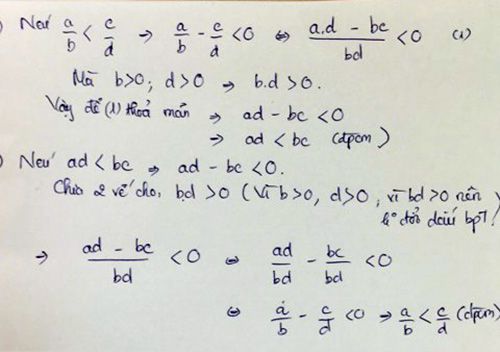
Làm nhắn gọn hơn thì
1
a/b < c/d
=> ad/bd < cb/db
=> ad < cb
2
ad < cb
=>ad /bd < cb/bd
Chúc pn hc tốt

a. Mẫu chung b.d > 0 (do b > 0; d > 0) nên nếu: thì da < bc
b. Ngược lại nếu a.d < b.c thì Ta có thể viết:
Bài 2: a. Chứng tỏ rằng nếu (b > 0; d > 0) thì
b. Hãy viết ba số hữu tỉ xen giữa và
Giải: a) Theo bài 1 ta có: (1)
Thêm a.b vào 2 vế của (1) ta có: a.b + a.d < b.c + a.b
a(b + d) < b(c + a) (2)
Thêm c.d vào 2 vế của (1): a.d + c.d < b.c + c.d
d(a + c) < c(b + d) (3) Từ (2) và (3) ta có:
a.d<b.c
Chúc bạn học tốt!!!! ^-^

1.
Nếu \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{ad}{bd}< \frac{cb}{db}\)
\(\Leftrightarrow ad< cd\left(dpcm\right)\)
2
Nếu \(ad< bc\Leftrightarrow\frac{ad}{bd}< \frac{bc}{bd}\)
\(\Leftrightarrow\frac{a}{b}< \frac{c}{d}\left(dpcm\right)\)

sửa lại : \(a=\frac{c}{d}\cdot b\Leftrightarrow a=\frac{b\cdot c}{d}\Leftrightarrow a\cdot d=b\cdot c\)
Mình nghĩ bài này không làm được vì a/b=c/d=>a.d=b.c là định nghĩa của phân số bằng nhau rồi(sai thì thôi nhé)

Ta có:a/b<c/d =>ad<bc (1)
Thêm ab vào (1) ta đc:
ad+ab<bc+ab hay a(b+d)<b(a+c) =>a/b<a+c/b+d (2)
Thêm cd vào 2 vế của (1), ta lại có:
ad+cd<bc+cd hay d(a+c)<c(b+d) => c/d>a+c/b+d (3)
Từ (2) và (3) suy ra:a/b<a+c/b+d<c/d
Áp dụng t/c dãy tỉ : a/b = b/c = c/d = (a + b + c)/(b + c + d). suy ra (a/b)^3 = (a+b+c/b+c+d)^3
Vậy (a+b+c/B+c+d)^3 = (a/b)^3 = (a/b).(a/b).a/b) = (a/b).(b/c).(c/d) = a/d (do rút gọn
Khuyến · 4 năm trước
dung ko ban