cho tứ giác ABCD có BA<BC,<B+<C=180o và BD là tia phân giác của góc ABC. CMR Tam giác ADC cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
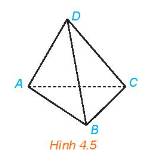
Có 4 mặt phẳng đi qua ba trong số bốn đỉnh của tứ giác đó là: (DAB), (DAC), (DBC), (ABC)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
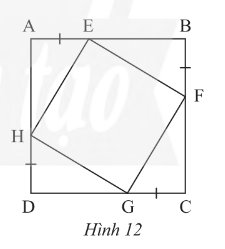
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) là một góc vuông
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
BX
Bùi Xuân Bảo
VIP
30 tháng 8
Hướng chung (các bước thường dùng)
- Xác định các tam giác vuông: Tìm các tam giác có một cạnh là nửa đường chéo, là trung tuyến, hoặc là một đường thẳng vuông góc được cho — dùng tính chất vuông/góc 45° (trong hình vuông) để kết luận các góc bằng nhau.
- Chứng minh 3 góc vuông của tứ giác \(E F G H\):
- Nếu bạn tìm được ba nghiệm của dạng “hai đoạn thẳng giao nhau vuông góc” tại ba đỉnh khác nhau, ghi lại lý do (ví dụ: hai đường là tiếp tuyến với cùng một đường tròn, hoặc là hai đường thẳng lần lượt song song/vuông góc với hai cạnh vuông góc của \(A B C D\)).
- Dùng quan hệ góc trong tam giác (tổng góc = \(180^{\circ}\)) để suy ra góc thứ tư nếu cần.
- Chứng minh \(H E = H G\): So sánh hai tam giác có chung cạnh/đồng dạng/đồng cạnh — thường dùng: nếu hai tam giác cân (có hai góc bằng nhau) hoặc đường trung trực, hoặc tia phân giác, thì hai cạnh tương ứng bằng nhau.
- Chứng minh \(A B C D\) là hình vuông (nếu chưa biết):
- Nếu biết \(A B \parallel C D\) và \(B C \parallel A D\) cộng thêm \(A B = B C\) hoặc một góc vuông, suy ra là hình chữ nhật có hai cạnh bằng → hình vuông.
- Hoặc chứng minh 4 góc đều \(90^{\circ}\) (qua tính song song/vuông góc) và một cặp cạnh bằng độ dài → hình vuông.
Ví dụ mẫu (nếu \(E , F , G , H\) là trung điểm các cạnh lần lượt của \(A B , B C , C D , D A\))
- a) Tứ giác \(E F G H\) là hình vuông (thế nên có 4 góc vuông chứ không phải chỉ 3): vì \(E F \parallel A D\) và \(F G \parallel A B\) nên \(E F \bot F G\), v.v.
- b) \(H E = H G\): do đối xứng theo tâm hình vuông (các đoạn nối tâm đến các trung điểm bằng nhau).
- c) \(A B C D\) là hình vuông: đây là giả thiết trong ví dụ này.