Tìm x, biết:
a) (x – 3) (2y + 1) = 7
b) (2x + 1) (3y – 2) = - 55.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
13 tháng 10 2021
\(\dfrac{x}{-3}=\dfrac{y}{5}\)⇒\(\dfrac{x}{-6}=\dfrac{y}{10}\)
\(\dfrac{y}{2}=\dfrac{z}{7}\)⇒\(\dfrac{y}{10}=\dfrac{z}{35}\)
⇒\(\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}\)
⇒\(\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{z}{35}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{z}{35}=\dfrac{2x-3y+z}{-12-30+35}=\dfrac{42}{-7}=-6\)
⇒\(\left\{{}\begin{matrix}x=-6.-6=36\\y=-6.10=-60\\z=-6.35=-210\end{matrix}\right.\)
13 tháng 10 2021
\(a,\dfrac{x}{-3}=\dfrac{y}{5}\Rightarrow\dfrac{x}{-6}=\dfrac{y}{10};\dfrac{y}{2}=\dfrac{z}{7}\Rightarrow\dfrac{y}{10}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{-6}=\dfrac{y}{10}=\dfrac{z}{35}=\dfrac{2x}{-12}=\dfrac{3y}{30}=\dfrac{2x-3y+z}{-12-30+35}=\dfrac{42}{-7}=-6\\ \Rightarrow\left\{{}\begin{matrix}x=36\\y=-60\\z=-210\end{matrix}\right.\)
\(b,6x=4y=z\Rightarrow\dfrac{6x}{12}=\dfrac{4y}{12}=\dfrac{z}{12}\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{12}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{12}=\dfrac{2x}{4}=\dfrac{3y}{9}=\dfrac{2x-3y+z}{4-9+12}=\dfrac{42}{7}=6\\ \Rightarrow\left\{{}\begin{matrix}x=12\\y=18\\z=72\end{matrix}\right.\)
\(c,x=-2y\Rightarrow\dfrac{x}{-2}=y\Rightarrow\dfrac{x}{-4}=\dfrac{y}{2}\\ 7y=2z\Rightarrow\dfrac{y}{2}=\dfrac{z}{7}\\ \Rightarrow\dfrac{x}{-4}=\dfrac{y}{2}=\dfrac{z}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{-4}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{2x}{-8}=\dfrac{3y}{6}=\dfrac{2x-3y+z}{-8+6+7}=\dfrac{42}{5}\\ \Rightarrow\left\{{}\begin{matrix}x=-\dfrac{168}{5}\\y=\dfrac{84}{5}\\z=\dfrac{294}{5}\end{matrix}\right.\)
H
1
7 tháng 2 2022
a) \(\left(x+1\right)\left(y+4\right)=7\).
-Vì \(x,y\in Z\) nên ta có thể viết:
\(\left(x+1\right)\left(y+4\right)=1.7\) hay \(\left(x+1\right)\left(y+4\right)=7.1\) hay \(\left(x+1\right)\left(y+4\right)=\left(-1\right).\left(-7\right)\) hay \(\left(x+1\right)\left(y+4\right)=\left(-7\right).\left(-1\right)\)
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=1.7\):
\(\Rightarrow x+1=1\) và \(y+4=7\)
\(\Rightarrow x=0\left(tmđk\right)\) và \(y=3\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=7.1\):
\(\Rightarrow x+1=7\) và \(y+4=1\)
\(\Rightarrow x=6\left(tmđk\right)\) và \(y=-3\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=\left(-1\right).\left(-7\right)\):
\(\Rightarrow x+1=-1\) và \(y+4=-7\)
\(\Rightarrow x=-2\left(tmđk\right)\) và \(y=-11\left(tmđk\right)\).
+Xét trường hợp \(\left(x+1\right)\left(y+4\right)=\left(-7\right).\left(-1\right)\):
\(\Rightarrow x+1=-7\) và \(y+4=-1\)
\(\Rightarrow x=-8\left(tmđk\right)\) và \(y=-5\left(tmđk\right)\).
b) \(xy+2x-3y=-1\)
\(\Rightarrow xy+2x-3y+1=0\)
\(\Rightarrow y\left(x-3\right)=-2x-1\)
\(\Rightarrow y=-\dfrac{2x+1}{x-3}=\dfrac{2\left(x-3\right)-5}{x-3}=2-\dfrac{5}{x-3}\)
-Vì \(y\in Z\) \(\Rightarrow5⋮\left(x-3\right)\).
\(\Rightarrow\left(x-3\right)\inƯ\left(5\right)\)
\(\Rightarrow x-3\in\left\{1;-1;5;-5\right\}\)
\(\Rightarrow x\in\left\{4;2;8;-2\right\}\) (đều thỏa mãn điều kiện).
+Với \(x=4\) thì \(y=\dfrac{5}{4-3}=5\) (tmđk).
+Với \(x=2\) thì \(y=\dfrac{5}{2-3}=-5\) (tmđk).
+Với \(x=8\) thì \(y=\dfrac{5}{8-3}=1\) (tmđk)
+Với \(x=-2\) thì \(y=\dfrac{5}{-2-3}=-1\) (tmđk).
K
0
12 tháng 10 2021
Bài 2:
a: \(3x^2-3xy=3x\left(x-y\right)\)
b: \(x^2-4y^2=\left(x-2y\right)\left(x+2y\right)\)
c: \(3x-3y+xy-y^2=\left(x-y\right)\left(3+y\right)\)
d: \(x^2-y^2+2y-1=\left(x-y+1\right)\left(x+y-1\right)\)
PT
Phạm Trần Hoàng Anh
CTVHS
25 tháng 6 2021
a) 3/35 - (3/5 + x) = 2/7
=> 3/5 + x= 3/35- 2/7
=> 3/5 +x = -1/5
=> x = -1/5 -3/5
=> x = -4/5
b) 3/7 +1/7 : x = 3/14
=> 1/7 : x= 3/14 -3/7
=> 1/7 : x = -3/14
=> x = 1/7 : -3/14
=> x = -2/3
c) (5x-1).(2x-1/3)=0
=> \(\left[{}\begin{matrix}5x-1=0\\2x-\dfrac{1}{3}=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}5x=0+1=1\\2x=0+\dfrac{1}{3}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=\dfrac{1}{3}:2=\dfrac{1}{6}\end{matrix}\right.\)
Học tốt :D
25 tháng 6 2021
a)x=-4/5
b)x=-2/3
c)\(\left\{{}\begin{matrix}5x-1=0\\2x-\dfrac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=1\\2x=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\x=\dfrac{1}{6}\end{matrix}\right.\)
Vậy.........
mik lười mong bn thông cảm
10 tháng 7 2023
a: A=2/3x^2y+4x^2y=14/3x^2y
=14/3*9*7=294
b: B=xy^2(1/2+1/3+1/6)=xy^2=3/4*1/4=3/16
c: C=x^3y^3(2+10-20)=-8x^3y^3
=-8*1^3(-1)^3=8
d: D=xy^2(2018+16-2016)
=18xy^2
=18(-2)*1/9=-4
NT
0
CM
4 tháng 5 2019
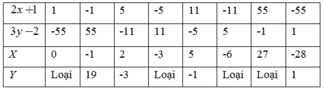
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
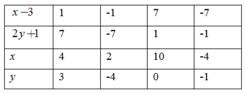
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.
TH
0
a) \(\left(x-3\right)\left(2y+1\right)=7\Rightarrow x-3;2y+1\)là cặp ước của 7
Ta có: \(Ư\left(7\right)=\left\{1;7;-1;-7\right\}\)
Nếu \(\hept{\begin{cases}x-3=1\\2y+1=7\end{cases}\Rightarrow\hept{\begin{cases}x=4\\y=3\end{cases}}}\)
Nếu \(\hept{\begin{cases}x-3=7\\2y+1=1\end{cases}\Rightarrow}\hept{\begin{cases}x=10\\y=0\end{cases}}\)
Nếu \(\hept{\begin{cases}x-3=-1\\2y+1=-7\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y=-4\end{cases}}}\)
Nếu \(\hept{\begin{cases}x-3=-7\\2y+1=-1\end{cases}\Rightarrow\hept{\begin{cases}x=-4\\y=-1\end{cases}}}\)
Vậy \(\left(x;y\right)\in\left\{\left(4;3\right);\left(10;0\right);\left(2;-4\right);\left(-4;-1\right)\right\}\)
b) \(\left(2x+1\right)\left(3y-2\right)=-55\Rightarrow2x+1;3y-2\)là cặp ước của -55
Ta có: \(Ư\left(-55\right)=\left\{1;5;11;55;-1;-5;-11;-55\right\}\)
Ta có bảng sau: \(\left(x;y\in Z\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(0;19\right);\left(27;1\right);\left(-3;-3\right);\left(-6;-1\right)\right\}\)
a) (x - 3)(2y + 1) = 7
=> x - 3 và 2y + 1 là các ước của 7
Ư(7) = {1; -1; 7; -7}
Lập bảng giá trị:
Đối chiếu điều kiện x, y là các số nguyên
=> Các cặp (x, y) cần tìm là:
(4; 3); (10; 0); (-2; -4); (-4; -1).