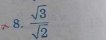 trục căn thức ở mẫu giúp mình v ạ mình camonn
trục căn thức ở mẫu giúp mình v ạ mình camonn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(a+b-2sqrt(ab))/(sqrt a-sqrtb)`
`= (sqrta-sqrtb)^2/(sqrta-sqrtb)`
`= sqrt a- sqrt b`
`(1+a sqrt a)/(1 + sqrt a)`
`= ((1+sqrta)(1-sqrta+a))/(1+sqrta)`
`= a - sqrt a +1`

`(a+4 sqrt a +4)/(sqrt a+2)`
`= (sqrt a+2)^2/(sqrt a+2)`
`= sqrt a +2`
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}=\sqrt{a}+2\)

2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2

Bài 1:
a.
\(\frac{1}{2\sqrt{2}-3\sqrt{3}}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2}-3\sqrt{3})(2\sqrt{2}+3\sqrt{3})}=\frac{2\sqrt{2}+3\sqrt{3}}{(2\sqrt{2})^2-(3\sqrt{3})^2}=\frac{2\sqrt{2}+3\sqrt{3}}{-19}\)
b.
\(=\sqrt{\frac{(3-\sqrt{5})^2}{(3-\sqrt{5})(3+\sqrt{5})}}=\sqrt{\frac{(3-\sqrt{5})^2}{3^2-5}}=\sqrt{\frac{(3-\sqrt{5})^2}{4}}=\sqrt{(\frac{3-\sqrt{5}}{2})^2}=|\frac{3-\sqrt{5}}{2}|=\frac{3-\sqrt{5}}{2}\)
Bài 2.
a.
\(=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{2\sqrt{2}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(=\sqrt{\frac{(2-\sqrt{3})^2}{(2-\sqrt{3})(2+\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)

a: \(\dfrac{6}{5\sqrt{8}}=\dfrac{6}{10\sqrt{2}}=\dfrac{3}{5\sqrt{2}}=\dfrac{3\sqrt{2}}{10}\)
b: \(\dfrac{7}{5+2\sqrt{3}}=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
c: \(\dfrac{6}{\sqrt{7}-\sqrt{5}}=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}=3\left(\sqrt{7}+\sqrt{5}\right)\)
a) \(\dfrac{6}{5\sqrt{8}}\)
\(=\dfrac{6}{5\cdot2\sqrt{2}}\)
\(=\dfrac{6}{10\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{5\sqrt{2}\cdot\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{10}\)
b) \(\dfrac{7}{5+2\sqrt{3}}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{\left(5+2\sqrt{3}\right)\left(5-2\sqrt{3}\right)}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{5^2-\left(2\sqrt{3}\right)^2}\)
\(=\dfrac{7\left(5-2\sqrt{3}\right)}{13}\)
\(=\dfrac{35-14\sqrt{3}}{13}\)
c) \(\dfrac{6}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}\)
\(=\dfrac{6\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=3\sqrt{7}+3\sqrt{5}\)

Bạn nói trục căn thức ở mẫu là sao, mik ko hiểu. Xin lỗi vì mik ko thể giải thích cho bạn được nha.

\(A=\frac{1}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{24}-\sqrt[3]{243}+\sqrt[3]{375}}\)
\(=\frac{1}{\sqrt[3]{9}-\sqrt[3]{3}+\sqrt[3]{8.3}-\sqrt[3]{27.9}+\sqrt[3]{125.3}}\)
\(=\frac{1}{\sqrt[3]{9}-\sqrt[3]{3}+2\sqrt[3]{3}-3\sqrt[3]{9}+5\sqrt[3]{3}}\)
\(=\frac{1}{6\sqrt[3]{3}-2\sqrt[3]{9}}=\frac{1}{2\sqrt[3]{9}.\left(\sqrt[3]{9}-1\right)}\)
\(=\frac{\sqrt[3]{81}.\left(\sqrt[3]{81}+\sqrt[3]{9}+1\right)}{2\sqrt[3]{9}.\left(\sqrt[3]{9}-1\right)\left(\sqrt[3]{81}+\sqrt[3]{9}+1\right).\sqrt[3]{81}}\)
\(=\frac{9\sqrt[3]{9}+9+3\sqrt[3]{3}}{144}\)
p/s: mk k chắc, sai đâu mn ib cho mk nhé
 trục căn thức ở mẫu giúp mình v ạ
trục căn thức ở mẫu giúp mình v ạ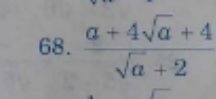 trục căn thức ở mẫu giúp mình v a
trục căn thức ở mẫu giúp mình v a
\(8.\dfrac{\sqrt{3}}{\sqrt{2}}=8.\dfrac{\sqrt{3}.\sqrt{2}}{\sqrt{2}.\sqrt{2}}=8.\dfrac{\sqrt{6}}{2}=4\sqrt{6}\)
\(\dfrac{\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{6}}{2}\)