Trên bảng có các số \(\frac{1}{96};\frac{2}{96};...;\frac{96}{96}.\)Mỗi một lần thực hiện, cho phép xóa đi hai số a,b bất kỳ trên bảng và thay bằng a+b-2ab. Hỏi sau 95 lần thực hiện phép xóa, số còn lại trên bảng có giá trị bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
Trần Hoàng Trung
VIP
5 tháng 9
Để giải bài toán này, ta cần tìm số lượng phân số mà chỉ sử dụng hai chữ số khác nhau trong các phân số được viết dưới dạng:
\(\frac{1}{98} , \frac{2}{97} , \frac{3}{96} , \ldots , \frac{98}{1}\)
Bước 1: Phân tích dãy phân số
Các phân số trong dãy có dạng:
\(\frac{1}{98} , \frac{2}{97} , \frac{3}{96} , \ldots , \frac{98}{1}\)
Ta thấy rằng các phân số này có tử số là các số từ 1 đến 98, và mẫu số là các số từ 98 đến 1. Cụ thể, phân số thứ \(i\) có tử số \(i\) và mẫu số \(99 - i\).
Vì vậy, ta có thể viết các phân số theo cặp như sau:
\(\frac{1}{98} , \frac{2}{97} , \frac{3}{96} , \ldots , \frac{98}{1}\)
Bước 2: Tìm các phân số chỉ sử dụng đúng hai chữ số khác nhau
Mỗi phân số có tử số và mẫu số là các số trong khoảng từ 1 đến 98. Để phân số này chỉ sử dụng hai chữ số khác nhau, tử số và mẫu số của phân số phải bao gồm đúng hai chữ số khác nhau.
Chúng ta sẽ xem xét các cặp số có tử số và mẫu số chỉ có hai chữ số khác nhau. Các cặp này có dạng \(\frac{x}{99 - x}\), trong đó \(x\) và \(99 - x\) phải có đúng hai chữ số khác nhau.
Bước 3: Xác định các cặp \(x\) và \(99 - x\)
Tử số và mẫu số là các số trong khoảng từ 1 đến 98. Để tìm các cặp số có đúng hai chữ số khác nhau, ta chỉ cần kiểm tra các giá trị của \(x\) sao cho \(x\) và \(99 - x\) có đúng hai chữ số khác nhau. Ta có thể thực hiện kiểm tra trực tiếp hoặc tính toán với các số cụ thể.
Bước 4: Đếm số lượng cặp
Sau khi kiểm tra các cặp, ta sẽ đếm được số lượng phân số chỉ sử dụng đúng hai chữ số khác nhau.
24 tháng 3 2022
Dễ thấy trong 2019 số trên có 1 số là \(-\dfrac{673}{2019}=-\dfrac{1}{3}\)
Khi xoá 1 số bất kì x khác -1/3 thuộc dãy số đó với số -1/3 ta được số mới là
\(x+3x.\dfrac{-1}{3}+\left(-\dfrac{1}{3}\right)=-\dfrac{1}{3}\)
Như vậy, sau khi xoá đủ 2018 lần thì số còn lại vẫn là -1/3
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a)
Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)
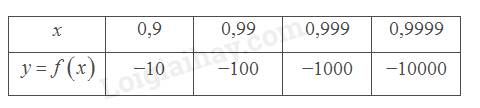
Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.
Số ở giữa của dãy là 1/2.
Do vậy nếu ta xóa số a,b bất kỳ thì ra một số mới nào đó ( đặt số mới là t chẳng hạn ) , đến một lúc nào đó sẽ phải xóa tới số 1/2 mà khi đó ta có :
t + 1/2 - 2 1/2t = 1/2
Do vậy số cuối cùng còn lại bất kể mọi cách xóa là 1/2 nhé.