Chứng minh rằng nếu: a2 \(⋮\)2 thì a\(⋮\)2 (a\(\varepsilon\)N)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh

\(a+b=1=>b=1-a\)
\(=>a^2+\left(1-a\right)^2\ge\dfrac{1}{2}\)
\(=>a^2+1-2a+a^2\ge\dfrac{1}{2}\)
\(\Leftrightarrow-2a+2a^2+1\ge\dfrac{1}{2}\)
\(\Leftrightarrow\left(-2a+2a^2+1\right).2\ge1\)
\(\Leftrightarrow-4a+4a^2+2\ge1\)
\(\Leftrightarrow-4a+4a^2+1\ge0\)
\(\Leftrightarrow\left(2a-1\right)^2\ge0\left(đúng\right)\)
\(''=''\left(khi\right)2a-1=0=>a=\dfrac{1}{2}\)
Ta có: \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2+a^2+b^2\ge2ab+a^2+b^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge1\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(đpcm\right)\)

Với mọi số thực ta luôn có:
`(a-b)^2>=0`
`<=>a^2-2ab+b^2>=0`
`<=>a^2+b^2>=2ab`
`<=>2(a^2+b^2)>=(a+b)^2=1`
`<=>a^2+b^2>=1/2(đpcm)`
Dấu "=' `<=>a=b=1/2`
ta có:
(a²+b²)(1²+1²)≥(a.1+b.1)²
⇔ 2(a²+b²) ≥ (a+b)²
⇔ 2(a²+b²)≥ 1 (vì a+b=1)
⇔ a² +b² ≥ 1/2 (đpcm)
dấu "=) xảy ra khi a = b = 1/2

Ta có
( a - b) ² >= 0
<=> a² - 2ab + b² >= 0
<=> a² + b² >=2ab
<=> 2 ( a² + b² ) >= a² +2ab + b²
<=> 2 (a² + b² ) >= ( a + b )² mà a+b=1 nên 2 ( a² + b² ) >=1
<=> a² + b² >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2

Với mọi số thực ta luôn có:
`(a-b)^2>=0`
`<=>a^2-2ab+b^2>=0`
`<=>a^2+b^2>=2ab`
`<=>2(a^2+b^2)>=(a+b)^2=1`
`<=>a^2+b^2>=1/2(đpcm)`
Dấu "=' `<=>a=b=1/2`
ta có:
(a²+b²)(1²+1²)≥(a.1+b.1)²
⇔ 2(a²+b²) ≥ (a+b)²
⇔ 2(a²+b²)≥ 1 (vì a+b=1)
⇔ a² +b² ≥ 1/2 (đpcm)
dấu "=) xảy ra khi a = b = 1/2
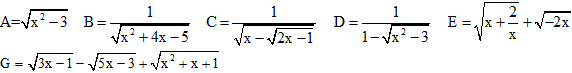 Mn giúp em với ;-;
Mn giúp em với ;-;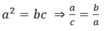
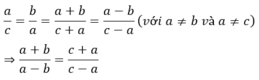
Vì \(a^2⋮2\)=) \(a^2\)là số chẵn
=) \(a\)là số chẵn =) \(a⋮2\)( Đpcm )
vì a^2 chia het cho 2 nen a là số chan
ma so chan thi se chia het cho 2