Giá trị nhỏ nhất của biểu thức 3x2 + y2 + 2xy + 4x là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)

Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2

\(A=\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+4\\ A=\left(x-y\right)^2+\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=1\end{matrix}\right.\Leftrightarrow x=y=1\)

\(A=3x^2+y^2+2xy+4x\)
\(=\left(2x^2+4x+2\right)+\left(x^2+y^2+2xy\right)-2\)
\(=2\left(x^2+2x+1\right)+\left(x+y\right)^2-2\)
\(=2\left(x+1\right)^2+\left(x+y\right)^2-2\)
Dễ thấy: \(2\left(x+1\right)^2+\left(x+y\right)^2\ge0\)
\(\Rightarrow2\left(x+1\right)^2+\left(x+y\right)^2-2\ge-2\)
Xảy ra khi \(\hept{\begin{cases}x+1=0\\x+y=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-1\\x=-y\end{cases}}\Rightarrow x=-y=-1\)

\(A=x^2+y^2+\left(\dfrac{1}{2}\right)^2-2xy+2.\dfrac{1}{2}x-2.\dfrac{1}{2}.y+\dfrac{3}{4}\)
\(A=\left(x-y+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(A_{min}=\dfrac{3}{4}\) khi \(x-y+\dfrac{1}{2}=0\)

\(C=2x^2+y^2-4x+2xy+1\)
\(=\left(x^2+2xy+y^2\right)+\left(x^2-4x+4\right)-3\)
\(=\left(x+y\right)^2+\left(x-2\right)^2-3\ge-3\)
-Dấu bằng xảy ra khi và chỉ khi \(x=2\) và \(y=-2\).

Chọn B.
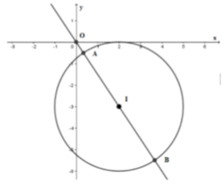
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
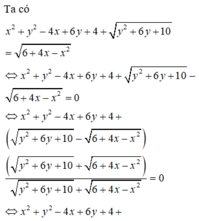
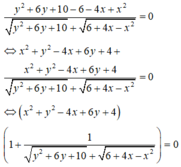


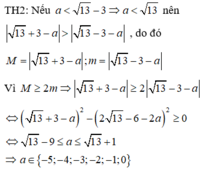

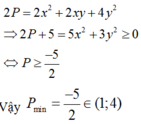
Đặt \(A=3x^2+y^2+2xy+4x\)
\(\Leftrightarrow A=y^2+2xy+x^2+2x^2+4x+2-2\)
\(\Leftrightarrow A=\left(x+y\right)^2+2\left(x+1\right)^2-2\)
Vì \(\left(x+y\right)^2\ge0;2\left(x+1\right)^2\ge0\)
\(\Rightarrow\left(x+y\right)^2+2\left(x+1\right)^2-2\ge-2\)
Dấu = xảy ra khi \(\hept{\begin{cases}x+y=0\\x+1=0\end{cases}\Rightarrow}\hept{\begin{cases}y=1\\x=-1\end{cases}}\)
Vậy Min A=-2 khi \(y=1;x=-1\)
\(3x^2+y^2+2xy+4x\)
\(=x^2+2xy+y^2+2x^2+4x+2-2\)
\(=\left(x+y\right)^2+2.\left(x+1\right)^2-2\ge-2\)
Dấu bằng xảy ra khi
\(\hept{\begin{cases}x=-y\\x=-1\end{cases}\Leftrightarrow\hept{\begin{cases}y=1\\x=-1\end{cases}}}\)
Vậy Min \(3x^2+y^2+2xy+4x\)=2 khi x=-1;y=1