Tìm :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lưu ý trước khi giải này: Số thập phân mình dùng / để ngăn cách tử và mẫu; còn kí hiệu nhân là x chứ không phải * và kí hiệu chia là : chứ không phải /.
Cách giải như sau:
1/11 x (1111/1212 + 1111/2020 + 1111/3030 + 1111/4242 + 1111/5656)
= 1/11 x (1111 : 101/1212 : 101 + 1111 : 101/2020 : 101 + 1111 : 101/3030 : 101 + 1111 : 101/4242 : 101 + 1111 : 101/5656 : 101)
= 1/11 x (11/12 + 11/20 + 11/30 + 11/42 + 11/56)
= 1/11 x 11(1/3x4 +1/4x5 + 1/5x6 + 1/6x7 + 1/7x8)
Ở đây vì vừa lấy 1 chia 11 (phân số là phép chia) và sau đó nhân tiếp với 11 nên lược bỏ vì 1 : 11 x 11 cũng = 1 thôi. Nên:
= 1 x (1/3x4 +1/4x5 + 1/5x6 + 1/6x7 + 1/7x8)
= 1 x (1/3 -1/4 + 1/4 -1/5 + 1/5 -1/6 + 1/6 -1/7 + 1/7 - 1/8)
Trong biểu thức này, ta thấy trong ngoặc đơn phần "1/4 + 1/4 -1/5 + 1/5 -1/6 + 1/6 -1/7 + 1/7" đã tự cộng trừ cho nhau và kết quả là 0. Do đó:
= 1 x (1/3 - 1/8)
= 1 x 5/24
= 5/24
Chúc bạn học tốt! k cho mình nha.

234123 x 1000 = 234123000
1212 + 12131 = 13343
4444 + 1111 = 5555
12121 + 10 = 12131


Bài này dễ thôi tham khảo nhé :)
Câu hỏi của ๖Eric Gaming - Toán lớp 4 - Học toán với OnlineMath

Lúc nãy, cô còn dạy học nên giờ cô mới giảng cho em được nhé.
B = (1 - \(\dfrac{1}{2}\))\(\times\)(1 - \(\dfrac{1}{3}\))\(\times\)(1 - \(\dfrac{1}{4}\))\(\times\)(1-\(\dfrac{1}{5}\))\(\times\)...\(\times\)(1- \(\dfrac{1}{2003}\))\(\times\)(1-\(\dfrac{1}{2004}\))
B = \(\dfrac{2-1}{2}\)\(\times\)\(\dfrac{3-1}{3}\)\(\times\)\(\dfrac{4-1}{4}\)\(\times\)\(\dfrac{5-1}{5}\)\(\times\)...\(\times\)(\(\dfrac{2003-1}{2003}\))\(\times\)(\(\dfrac{2004-1}{2004}\))
B = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{2}{3}\)\(\times\)\(\dfrac{3}{4}\)\(\times\)\(\dfrac{4}{5}\)\(\times\)...\(\times\)\(\dfrac{2002}{2003}\)\(\times\)\(\dfrac{2003}{2004}\)
B = \(\dfrac{2\times3\times4\times...\times2003}{2\times3\times4\times...\times2003}\)\(\times\) \(\dfrac{1}{2004}\)
B = \(\dfrac{1}{2004}\)

c: Ta có: \(\left|\dfrac{1}{2}x-2\right|-\left|x+3\right|=0\)
\(\Leftrightarrow\left|\dfrac{1}{2}x-2\right|=\left|x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-2=x+3\\\dfrac{1}{2}x-2=-x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\cdot\dfrac{-1}{2}=5\\x\cdot\dfrac{3}{2}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\\x=-\dfrac{2}{3}\end{matrix}\right.\)

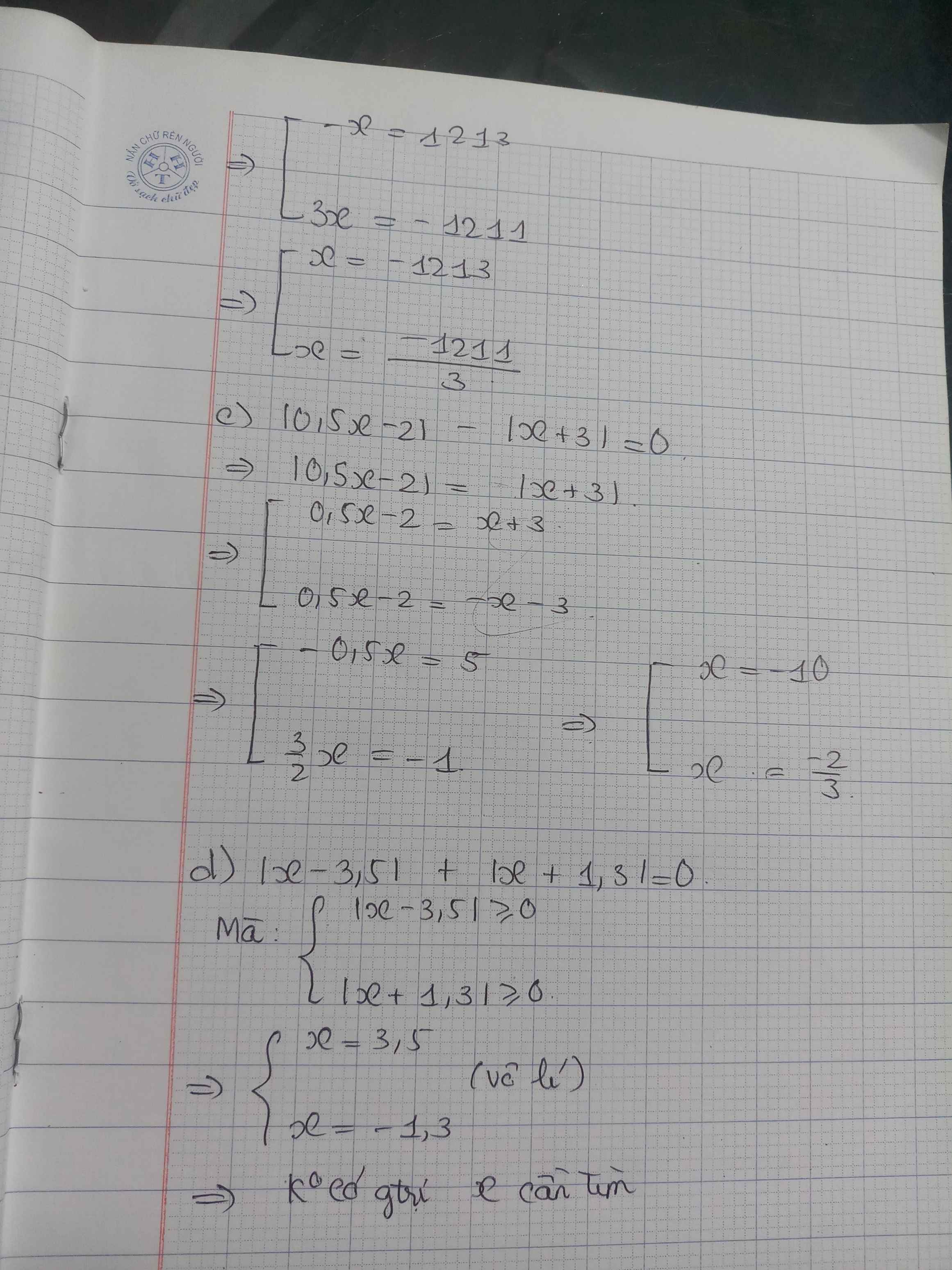
\(\dfrac{1}{3}\) + \(x\) = \(\dfrac{11}{12}\)
\(x\) = \(\dfrac{11}{12}\) - \(\dfrac{1}{3}\)
\(x\) = \(\dfrac{7}{12}\)