d) -x + 0,25x4 - 2x³: -0,5x²
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2021
c: Ta có: \(\left|\dfrac{1}{2}x-2\right|-\left|x+3\right|=0\)
\(\Leftrightarrow\left|\dfrac{1}{2}x-2\right|=\left|x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-2=x+3\\\dfrac{1}{2}x-2=-x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\cdot\dfrac{-1}{2}=5\\x\cdot\dfrac{3}{2}=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\\x=-\dfrac{2}{3}\end{matrix}\right.\)
HT
30 tháng 1 2018
a)(x-2)(2x-5)=0
=> x-2=0 hoặc 2x-5=0
=> x=2 x =\(\dfrac{5}{2}\)
Vậy S={2;\(\dfrac{5}{2}\)}
b)(0.2x-3)(0.5x-8)=0
=> 0,2x-3=0 hoặc 0,5x-8=0
=> x= 15 x = 16
Vậy s={15;16}
c)2x(x-6)+3(x-6)=0
=> (2x+3)(x-6)=0
=> 2x+3=0 hoặc x-6=0
=> x = -3/2 x = 6
Vậy x={-3/2;6}
d)(x-1)(2x-4)(3x-9)=0
=> 6(x-1)(x-2)(x-3)=0
=> x-1=0 hoặc x-2=0 hoặc x-3=0
=> x=1 x = 2 x=3
Vậy S={1;2;3}
Chúc bạn học tốt!
T
30 tháng 1 2018
a)(x-2)=0*
Hoặc (2x-5)=0**
giải (*) và(**)
(*)x=2
(**)x=5/2
b)(0.2x-3)=0 *'
Hoặc (0.5x-8)=0 *''
Giải(*') và(*'')
[Giải như trên]
C) 2x(x-6)+3(x-6)=0
<=>(2x+3)(x-6)=0
2x+3=0 **"
x-6=0 **"'
[Đến đây thì về dạng ban đầu]
d)
x-1=0 (1)
Hoặc 2x-4=0 (2)
Hoặc 3x-9=0 (3)
Giải (1);(2);(3)
[ như các phần trên 👆]
chúc bạn học tốt
9 tháng 1 2021
a) Ta có: \(7-\left(2x+4\right)=-\left(x+4\right)\)
\(\Leftrightarrow7-2x-4=-x-4\)
\(\Leftrightarrow-2x+3+x+4=0\)
\(\Leftrightarrow-x+7=0\)
\(\Leftrightarrow-x=-7\)
hay x=7
Vậy: S={7}
b) Ta có: \(\dfrac{2+x}{5}-0.5x=\dfrac{1-2x}{4}+0.25\)
\(\Leftrightarrow\dfrac{4\left(2+x\right)}{20}-\dfrac{0.5x\cdot20}{20}=\dfrac{5\left(1-2x\right)}{20}+\dfrac{20\cdot0.25}{20}\)
\(\Leftrightarrow4\left(2+x\right)-10x=5\left(1-2x\right)+5\)
\(\Leftrightarrow8+4x-10x=5-10x+5\)
\(\Leftrightarrow-6x+8=-10x+10\)
\(\Leftrightarrow-6x+8+10x-10=0\)
\(\Leftrightarrow4x-2=0\)
\(\Leftrightarrow4x=2\)
hay \(x=\dfrac{1}{2}\)
Vậy: \(S=\left\{\dfrac{1}{2}\right\}\)
d) Ta có: \(\dfrac{x-1}{59}+\dfrac{x-2}{58}+\dfrac{x-3}{57}=\dfrac{x-59}{1}+\dfrac{x-58}{2}+\dfrac{x-57}{3}\)
\(\Leftrightarrow\dfrac{x-1}{59}-1+\dfrac{x-2}{58}-1+\dfrac{x-3}{57}-1=\dfrac{x-59}{1}-1+\dfrac{x-58}{2}-1+\dfrac{x-57}{3}-1\)
\(\Leftrightarrow\dfrac{x-60}{59}+\dfrac{x-60}{58}+\dfrac{x-60}{57}=\dfrac{x-60}{1}+\dfrac{x-60}{2}+\dfrac{x-60}{3}\)
\(\Leftrightarrow\left(x-60\right)\left(\dfrac{1}{59}+\dfrac{1}{58}+\dfrac{1}{57}\right)-\left(x-60\right)\left(1+\dfrac{1}{2}+\dfrac{1}{3}\right)=0\)
\(\Leftrightarrow\left(x-60\right)\left(\dfrac{1}{59}+\dfrac{1}{58}+\dfrac{1}{57}-1-\dfrac{1}{2}-\dfrac{1}{3}\right)=0\)
mà \(\dfrac{1}{59}+\dfrac{1}{58}+\dfrac{1}{57}-1-\dfrac{1}{2}-\dfrac{1}{3}\ne0\)
nên x-60=0
hay x=60
Vậy: S={60}
NT
0
1 tháng 2 2022
a: =>3y=6x-1
=>y=2x-1/3
Vậy: (a)//(e)
b: y=-0,5x-4
c: y=1/2x+3
d: =>2y=6-x
=>2y=(6-x)/2=-0,5x+3
f: =>y=0,5x+1=1/2x+1
Vậy: (c)//(f), (d)//(b)
VN
1
KV
1 tháng 5 2023
0,5x(2x - 9) = 1,5x(x - 5)
⇔ x² - 4,5x = 1,5x² - 7,5x
⇔ x² - 1,5x² + 7,5x - 4,5x = 0
⇔ -0,5x² + 3x = 0
⇔ 0,5x(-x + 6) = 0
⇔ 0,5x = 0 hoặc -x + 6 = 0
*) 0,5x = 0
⇔ x = 0
*) -x + 6 = 0
⇔ -x = -6
⇔ x = 6
Vậy S = {0; 6}
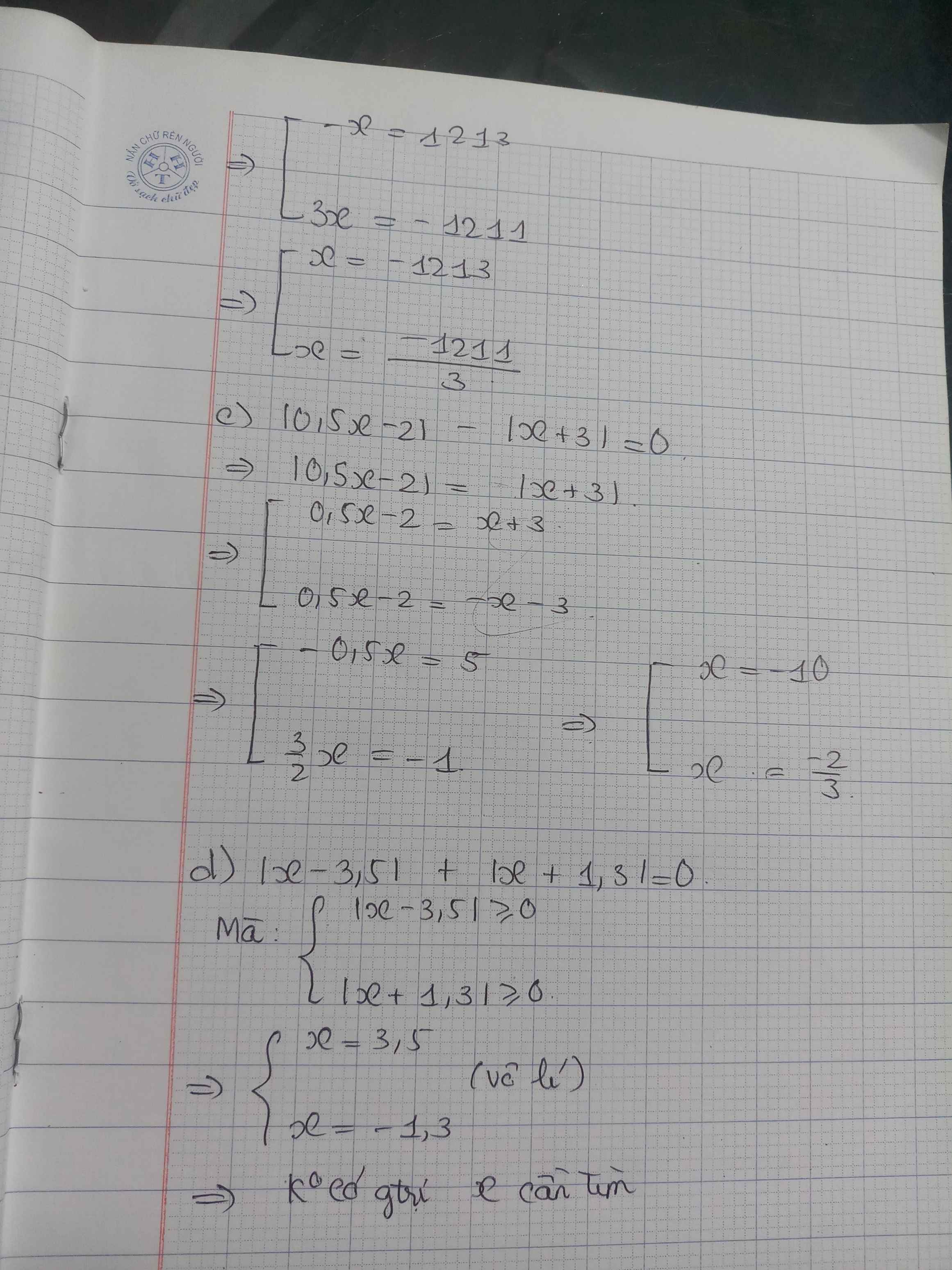
Thu gọn và sắp xếp đa thức
- \(x\) + 0,25\(\times\) 4 - 2\(x^3\) - 0,5\(x^2\)
= - \(x\) + 1 - 2\(x^3\) - 0,5\(x^2\)
= -2\(x^3\) - 0,5\(x^2\) - \(x\) + 1