làm thế nào x2 = x3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 6 2019
Lời giải của các bạn đều thỏa mãn yêu cầu đề bài là phân tích đa thức thành nhân tử
28 tháng 2 2019
Chọn đáp án D
(X1) C6H5NH2 Anilin có tính bazo rất yếu nên dung dịch của nó k thể làm xanh quỳ tím được ⇒ Loại X1
(X2) CH3NH2 Mrtyl amin có tính bazo mạnh hơn NH3 ⇒ Chọn X2
(X3) H2NCH2COOH Glyxin có số nhóm –NH2 và –COOH bằng nhau ⇒ pH ~ 7 ⇒ Loại X3
(X4) HOOCCH2CH2CH(NH2)COOH Axit Glutamic (Glu) có 2 nhóm –COOH và 1 nhóm –NH2 ⇒ dd của nó làm quỳ hóa hồng ⇒ Loại X4
(X5) H2NCH2CH2CH2CH2CH(NH2)COOH Lysin có 1 nhóm –COOH và 2 nhóm –NH2 ⇒ dd của nó làm quỳ hóa xanh ⇒ Chọn X5
4 tháng 8 2019
Chọn đáp án D.
(X1) C6H5NH2 Anilin có tính bazo rất yếu nên dung dịch của nó không thể làm xanh quỳ tím được.
⇒ Loại X1
(X2) CH3NH2 Mrtyl amin có tính bazơ mạnh hơn NH3
⇒ Chọn X2
(X3) H2NCH2COOH Glyxin có số nhóm –NH2 và –COOH bằng nhau.
⇒ pH ~ 7
⇒ Loại X3
(X4) HOOCCH2CH2CH(NH2)COOH Axit Glutamic (Glu) có 2 nhóm –COOH và 1 nhóm –NH2
⇒ Dung dịch của nó làm quỳ hóa hồng.
⇒ Loại X4
(X5) H2NCH2CH2CH2CH2CH(NH2)COOH Lysin có 1 nhóm –COOH và 2 nhóm –NH2
⇒ Dung dịch của nó làm quỳ hóa xanh.
⇒ Chọn X5
PT
1
CM
4 tháng 12 2017
Cách 1: Thực hiện phép chia
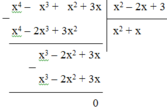
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3) = x2 + x
Cách 2: Phân tích x4 – x3 + x2 + 3x thành nhân tử có chứa x2 + x
x4 – x3 + x2 + 3x
= x.(x3 – x2 + x + 3)
= x.(x3 – 2x2 + 3x + x2 – 2x + 3)
= x.[x.(x2 – 2x + 3) + (x2 – 2x + 3)]
= x.(x + 1)(x2 – 2x + 3)
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3) = x(x + 1)
9 tháng 4 2017
Đáp án A
Từ NaNO 3 không thể tạo thành Na 2 CO 3 ; từ NaNO 3 không thể tạo thành NaOH . Vì thế chỉ có phương A là thỏa mãn.
Sơ đồ phản ứng :
12 tháng 2 2019
Đáp án A
C4H6O4: (HCOO)2C2H4
X2: C2H4(OH)2
X4: HCOOH
X: HOOC-COOCH2-CH2-OH
X1: (COONa)2
X3: (COOH)2
\(x^2\) = \(x^3\)
\(x^2\) - \(x^3\) = 0
\(x^2\).(1 - \(x\)) = 0
\(\left[{}\begin{matrix}x^2=0\\1-x=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(x\in\) { 0; 1}
cứu mình với