5x(x-2023)-x+2023
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét VT : x+3x+5x+7x+......+2023x
Số hạng của dãy số trên là : \(\dfrac{2023-1}{2}+1=1012\left(sốhạng\right)\)
Tổng số của dãy số trên là : \(\dfrac{\left(2023x+x\right).1012}{2}\text{=}1012x.1012\)
Do đó : ta có :
\(1012x.1012\text{=}2023.2024\)
\(1012x\text{=}4046\)
\(x\text{=}\dfrac{2023}{506}\)
VT = x + 3x + 5x + 7x +... + 2023x = [(2023 - 1):2 +1] . (2023+1)x = 1012. 2024x = 2048288x
VP= 2023 . 2024= 4094552
VT=VP <=> 2048288x =4094552
<=>\(x\approx2\)

\(5x^2+2y^2+6xy-8x-4y+4=0\)
\(\Leftrightarrow4x^2+x^2+y^2+y^2+2xy+4xy-8x-4y+4=0\)
\(\Leftrightarrow\left(4x^2+y^2+4+4xy-8x-4y\right)+\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow\left[\left(2x\right)^2+4xy+y^2-4\left(2x+y\right)+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left[\left(2x+y\right)^2-2\cdot\left(2x+y\right)\cdot2+2^2\right]+\left(x+y\right)^2=0\)
\(\Leftrightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Ta có: \(\left\{{}\begin{matrix}\left(2x+y-2\right)^2\ge0\forall x,y\\\left(x+y\right)^2\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(2x+y-2\right)^2+\left(x+y\right)^2\ge0\forall x,y\)
Mặt khác: \(\left(2x+y-2\right)^2+\left(x+y\right)^2=0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}2x+y-2=0\\x+y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(-y\right)+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2y+y-2=0\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-y=2\\x=-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=2\end{matrix}\right.\)
Thay x,y vào P ta có:
\(P=2^{2023}+\left(-2\right)^{2023}=2^{2023}-2^{2023}=0\)
Vậy: ...

\(\dfrac{x-2023}{6}+\dfrac{x-2023}{10}+\dfrac{x-2023}{15}+\dfrac{x-2023}{21}=\dfrac{8}{21}\)
\(\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\left(x-2023\right).\dfrac{8}{21}=\dfrac{8}{21}\)
\(x-2023=1\)
\(x=2024\)
Vậy..............
\(...\Rightarrow\left(x-2023\right)\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right)\left(\dfrac{35+21+14+1}{210}\right)=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}\)
\(\Rightarrow\left(x-2023\right).\dfrac{71}{210}=\dfrac{8}{21}.\dfrac{210}{71}=\dfrac{80}{71}\)
\(\Rightarrow x-2023=\dfrac{80}{71}\Rightarrow x=\dfrac{80}{71}+2023=\dfrac{143713}{71}\)

\(2023\times28+2023\times34-2023\times52\)
\(=2023\times\left(28+34-52\right)\)
\(=2023\times10\)
\(=20230\)
`# \text {DNamNgV}`
`2023 \times 28 + 2023 \times 34 - 2023 \times 52`
`= 2023 \times (28 + 34 - 52)`
`= 2023 \times 10 `
`=20230`

\(y\times2023-y=2023\times2021+2023\)
\(y\times\left(2023-1\right)=2023\times\left(2021+1\right)\)
\(y\times2022=2023\times2022\)
\(y=2023\times2022\div2022\)
\(y=2023\)

2030 × 4 +2023 × 2 + 3 × 2023
=8120 + 4046 + 6069
=18235
= 4x2023+2023x2+2023 x1 + 3x2023
=2023x (4+2+3+1)
= 2023 x 10
= 20230
cảm ơn bạn đã đọc!

2023×6+7×2023−2023
=2023×6+7×2023−2023x1
=2023×(6+7−1)
=2023×12
=24276
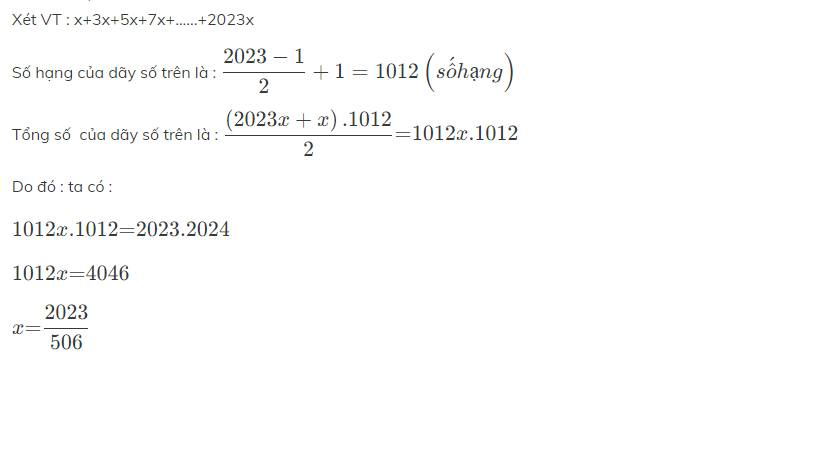
=5x(x-2023)-(x-2023)
=(x-2023)(5x-1)