cho đường thẳng (d) y=x và (d') y= - 2x + 3
a) Vẽ (D) và (D') trên cùng một mặt phẳng tọa độ Oxy b) tìm phương trình đường thẳng (d) song song với (d') và đi qua điểm n(0;5)c) chứng minh (D) và (D') tại M(1;1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 12 2021
a: Vì (d)//y=2x+3 nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=-1 vào (d), ta được:
b+2=-1
hay b=-3
N
3 tháng 12 2021
c. Gọi: \(\left[{}\begin{matrix}y=x+1\left(d'\right)\\y=\left(m-1\right)x+5\left(d''\right)\end{matrix}\right.\)
Ta có: \(PTHDGD:\left(d\right)-\left(d'\right)\)
\(2x+3=x+1\)
\(\Rightarrow x=-2\left(1\right)\)
\(Thay\left(1\right)in\left(d'\right):y=-2+1=-1\)
\(\Rightarrow A\left(-2;-1\right)\)
Để 3 đt này đồng quy, thì \(A\left(-2;-1\right)\in\left(d''\right)\Leftrightarrow-1=-2m+2+5\)
\(\Rightarrow m=4\)
30 tháng 11 2021
a: Vì (d)//y=2x+3 nên a=2
Thay x=1 và y=-1 vào y=2x+b, ta được:
b+2=-1
hay b=-3
30 tháng 11 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}a+b=-1\\a=2;b\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-3\end{matrix}\right.\\ c,\text{PT hoành độ giao điểm }\left(d\right)\text{ và }y=x+1\\ x+1=2x-3\Leftrightarrow x=4\Leftrightarrow y=5\Leftrightarrow A\left(4;5\right)\\ \text{Để 3 đt đồng quy thì }A\left(4;5\right)\in y=\left(m-1\right)x+5\\ \Leftrightarrow4m-4+5=5\Leftrightarrow m=1\)
CM
10 tháng 9 2017
Xét phương trình hoành độ giao điểm của d và d’ ta có:
2 x – 1 = x – 3 ⇔ x = − 2 ⇔ y = − 5 ⇔ M ( − 2 ; − 5 )
Trước hết xét M có thuộc đường thẳng y = 3 x + 1 không?
Ta có 3 . x M + 1 = 3 . ( − 2 ) + 1 = − 5 = y M nên M thuộc đồ thị hàm số y = 3 x + 1
hay A đúng
Đáp án cần chọn là: A
CM
30 tháng 6 2017
Chọn B
Gọi (P) là mặt phẳng chứa hai đường thẳng d₁ và d₂
Khi đó (P) đi qua M (0;-1;0) và có cặp véctơ chỉ phương 
Gọi 
là VTPT của (P). Khi đó 
Phương trình (P): -8x+3y+2z+3=0
Gọi H là giao điểm của đường thẳng d₂ và (P):
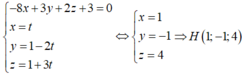
Đường thẳng d đi qua H và có VTCP 
có phương trình:
a: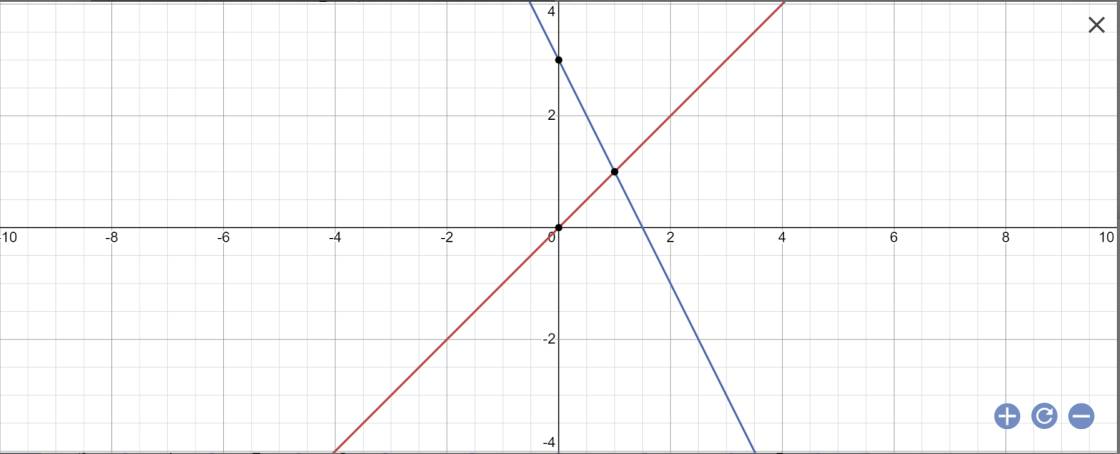
b: (d1)//(d')
=>(d1): y=-2x+b
Thay x=0 và y=5 vào (d1), ta được:
b-2*0=5
=>b=5
c: Tọa độ giao điểm là;
x=-2x+3 và y=x
=>3x=3 và y=x
=>x=1 và y=1(ĐPCM)