Bài 2. Cho tam giác ABC vuông tại A
a) Biết hai trung tuyến BN= 4cm; AM= 3cm. Tính các cạnh của tam giác ABC
b) Biết AB= a, hai đường trung tuyến AM, BN vuông góc với nhau. Tính hai cạnh AC, BC theo a
c) Biết BC= 2a, BM, CN là hai trung tuyến. Tính MB^2 + NC^2 theo a, từ đó tìm GTLN của MB+ NC theo a

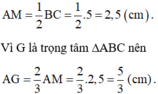
a)
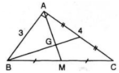
Có 2 trung tuyến BN, CM cắt nhau suy ra \(BN\perp AM\)
Gọi G là trọng tâm tam giác ABC, ta có \(BG=\dfrac{2}{3}BN=\dfrac{2}{3}.4=\dfrac{8}{3}\left(cm\right)\)
Trong tam giác ABN vuông tại A, đường cao AG, ta có:
\(AB^2=BG.BN\) (hệ thức lượng)
\(\Rightarrow AB=\sqrt{\dfrac{8}{3}.4}=\dfrac{4\sqrt{6}}{3}\left(cm\right)\)
Tam giác ABN vuông tại A
\(\Rightarrow AN^2=BN^2-AB^2\\ \Rightarrow AN=\sqrt{4^2-\left(\dfrac{4\sqrt{6}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Mà N là trung điểm AC => AC = \(\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
Áp dụng đl pytago vào tam giác ABC:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{4\sqrt{6}}{3}\right)^2+\left(\dfrac{8\sqrt{3}}{3}\right)^2}=4\sqrt{2}\left(cm\right)\)
Thừa dữ kiện AM = 3cm, bạn coi kỹ đề đủ/ đúng hết chưa thì cmt để chút mình coi lại bài giải