choΔABC (90 độ); BD là phân giác của góc B (DϵAC). trên tia BC lấy điểm E sao cho BA=BE
a, chứng minh ΔBAD=ΔBED
b)chứng minh BD là đường trung trực của AE.
c)Kẻ AH vuông góc BC . so sánh EH và EC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có: AM=MD (gt)
MC=MB(gt)
\(\widehat{AMC}=\widehat{BMD}\)( góc đối tạo bởi hai đường thẳng)
=> \(\Delta AMC=\Delta DMB\)(1)
b, (1) => AC=BD
c, Ta có: góc MAC= góc MBD ( ΔAMC=ΔDMB)
=> AC// BD
mà AC vuông góc AB => BD vuông góc AC

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó:ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
b: Xét tứ giác AMCE có
AM//CE
AE//CM
Do đó:AMCE là hình bình hành
mà MA=MC
nên AMCE là hình thoi

Dựng hình bình hành ABDC \(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
\(\left|\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{BA}+\overrightarrow{CB}\right|\)
\(\Leftrightarrow\left|\overrightarrow{AD}+\overrightarrow{MA}\right|=\left|\overrightarrow{MC}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MD}\right|=\left|\overrightarrow{MA}\right|\)
\(\Leftrightarrow MD=MA\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng AD

a; Xét ΔABC co AM/AB=AN/AC
nên MN//BC
=>ΔAMN đồng dạng với ΔBAC
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMN}=30\left(cm^2\right)\)
b: MN/BC=AM/AB=1/2

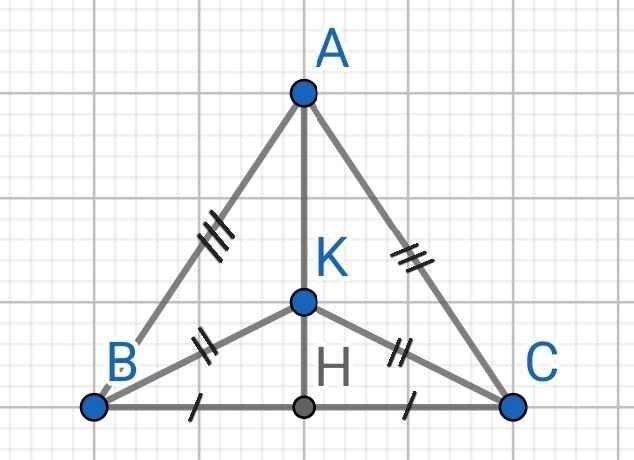
∆ABC cân tại A
⇒ H là trung điểm BC
⇒ AH là đường trung trực của ABC
⇒ AH là đường trung trực của BC
Ta có:
KB = KC (gt)
⇒ K nằm trên đường trung trực của BC
Mà AH là đường trung trực của BC
⇒ K ∈ AH
⇒ A, K, H thẳng hàng

x y A E D C B 1 3 2 1
a)
A1^ + A2^ + A3^ = EAD^
(A1^ + A2^) + 90o = 180o
A1^ + A2^= 90o
=> A2^= 90o- A1^ (1)
mà C1^ + A1^=90o (phụ nhau)
=> C1^ = 90o - A1^ (2)
Từ (1) và (2) => A2^ = C1^
b)
Xét \(\Delta\)CEA và \(\Delta\)ADB :
CEA^ = ADB^ = 90o
AC = AB (do \(\Delta\)ABC vuông cân tại A)
C1^ = A2^ (cmt)
=> \(\Delta\)CEA = \(\Delta\)ADB (cạnh huyền_ góc nhọn)
=> CE= AD (2 cạnh tương ứng)
BD = AE (2 cạnh tương ứng)
Ta có:
DE = EA + AD = BD + CE ( đpcm)
Cũng vẫn đề bài và câu hỏi như trên nhưng B,C nằm khác phía vs xy
Giúp mình vs mn với @Cold Wind vẽ hình giúp lun nka ![]()
b,xét tam giác BAE có BA=BE(Gt)
⇒
⇒tam giac BAE Cân tại B
Mà BD là dường phân giác
⇒
⇒BD đồng thời là đường trung trực của AE
C suy ra góc HAE bằng góc DAE
xét tam giác HAE và tam giác KAE:
.AE là cạnh huyền chung
.góc HAE bằng góc DAE
suy ra :tam giác HAE = tam giác KAE( ch-gn)
suy ra EH=EK (1)
Ta lại có tam giác EKC vuông tại K nên:
EK<EC( cạnh góc vuông bé hơn cạnh huyền) (2)
Từ (1) và (2) suy ra EH<EC
làm được mỗi 2 câu ko bt có đúng ko