tìm các giá trị nguyên của x và y biết 4xy - 10y + 6x = 22
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm được A = 24 5 và B = - 6 x - 4 với x > 0 và x ≠ 4 ta tìm được 0 < x < 1
Ta có M = - 1 + 2 x ∈ Z => x ∈ Ư(2) từ đó tìm được x=1

Ta có:
\(P=4x^2y^2-3xy^3+5x^2y^2-5xy^3-xy+x-1\)
\(P=\left(4x^2y^2+5x^2y^2\right)-\left(3xy^3+5xy^3\right)-xy+x-1\)
\(P=9x^2y^2-8xy^3-xy+x-1\)
Bậc của đa thức P là: \(2+2=4\)
Thay x=-1 và y=2 vào P ta có:
\(P=9\cdot\left(-1\right)^2\cdot2^2-8\cdot-1\cdot2^3-\left(-1\right)\cdot2+\left(-1\right)-1=100\)
\(Q=-4x^2y^2-xy+4xy^3+2xy-6x^3y-4x^3y\)
\(Q=-4x^2y^2-\left(xy-2xy\right)+4xy^3-\left(6x^3y+4x^3y\right)\)
\(Q=-4x^2y^2+xy+4xy^3-10x^3y\)
Bậc của đa thức Q là: \(2+2=4\)
Thay x=-1 và y=2 vào Q ta có:
\(Q=-4\cdot\left(-1\right)^2\cdot2^2+\left(-1\right)\cdot2+4\cdot-1\cdot2^3-10\cdot\left(-1\right)^3\cdot2=-30\)

+) \(x^2-4xy+5y^2=2\left(x-y\right)\Leftrightarrow x^2-2x\left(2y+1\right)+5y^2+2y=0\)
+) \(\Delta'=\left(2y+1\right)^2-5y^2-2y=-y^2+2y+1=-\left(y+1\right)^2+2\)
Do y nguyên và -(y+1)^2 >= -2 nên y+1 = 0, 1 hoặc -1 mà để delta chính phương thi y+1 = 1 hoặc -1 -> y = 0 hoặc -2
Từ đây thay lại vào và tìm được \(\left(x;y\right)\in\left\{\left(0;0\right)\right\}\)
\(x^2-4xy+5y^2=2\left(x-y\right)\)
\(\Leftrightarrow x^2-4xy+5y^2-2x+2y=0\)
\(\Leftrightarrow\left(x-2y\right)^2+2\left(x-2y\right)+1+y^2-2y+1=2\)
\(\Leftrightarrow\left(x-2y-1\right)^2+\left(y-1\right)^2=2\)
vì x,y là số nguyên nên ta có các trường hợp sau
th1: \(\hept{\begin{cases}x-2y-1=1\\y-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=2\end{cases}}}\)
th2 \(\hept{\begin{cases}x-2y-1=-1\\y-1=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=0\end{cases}}}\)
th3 \(\hept{\begin{cases}x-2y-1=-1\\y-1=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=2\end{cases}}}\)
th4 \(\hept{\begin{cases}x-2y-1=1\\y-1=-1\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}}\)

\(a,=\left(x^2y+3\right)^2\\ b,=\left(2x+y\right)^2\\ c,=\left(5y^2-1\right)^2\)

giải nhanh đi nhé mik cần gấp ai lm đủ đúng hết mik k mun cho nha giải đủ các bước nhé cảm ưn các bạn trước giúp mik nha^.^><hihiii
1) \(A=x^2+2x+3=\left(x+1\right)^2+2 \)
vi \(\left(x+1\right)^2\ge0\)(voi moi x)
\(\Rightarrow\left(x+1\right)^2+2\ge2\)(voi moi x)
Vay GTNN cua A =2 khi x=-1
2) Goi 2 so nguyen lien tiep do la x va x+1
TDTC x+1-x=1
Vi 1 la so le nen x+1-x la so le
Vay .......
3) \(\left(x-y\right)^2-\left(x+y\right)^2=\left(x-y-x-y\right)\left(x-y+x+y\right)\)
\(=-2y\cdot2x=-4xy\)(dpcm)
4) \(Q=-x^2+6x+1=-\left(x^2-6x-1\right)=-\left(x^2-6x+9-10\right)=-\left(x-3\right)^2+10\)
Vi \(\left(x-3\right)^2\ge0\)(voi moi x)
\(\Rightarrow-\left(x-3\right)^2\le0\)(voi moi x)
\(\Rightarrow-\left(x-3\right)^2+10\le10\)(voi moi x)
Vay GTLN cua Q=10 khi x=3

Lời giải:
$A=(x^2+4y^2+4xy)+y^2+6x+16y+32$
$=(x+2y)^2+6(x+2y)+(y^2+4y)+32$
$=(x+2y)^2+6(x+2y)+9+(y^2+4y+4)+19$
$=(x+2y+3)^2+(y+2)^2+19\geq 0+0+19=19$
Vậy $A_{\min}=19$. Giá trị này đạt tại $x+2y+3=y+2=0$
$\Leftrightarrow y=-2; x=1$
Giúp em với
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
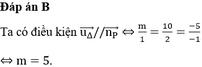
\(4xy+6x-10y=22\)
\(\Leftrightarrow4xy+6x-10y-15=7\)
\(\Leftrightarrow2x\left(2y+3\right)-5\left(2y+3\right)=7\)
\(\Leftrightarrow\left(2x-5\right)\left(2y+3\right)=7\)
Vậy \(\left(x;y\right)=\left(-1;-2\right);\left(2;-5\right);\left(3;2\right);\left(6;-1\right)\)