Cho tam giác ABC cân ở A, có 𝐴𝐵 = 10𝑐𝑚,𝐵𝐶 = 12𝑐𝑚. Tính độ dài phân giác AD của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
21 tháng 3 2023
Đúng(1)
Những câu hỏi liên quan
22 tháng 12 2021
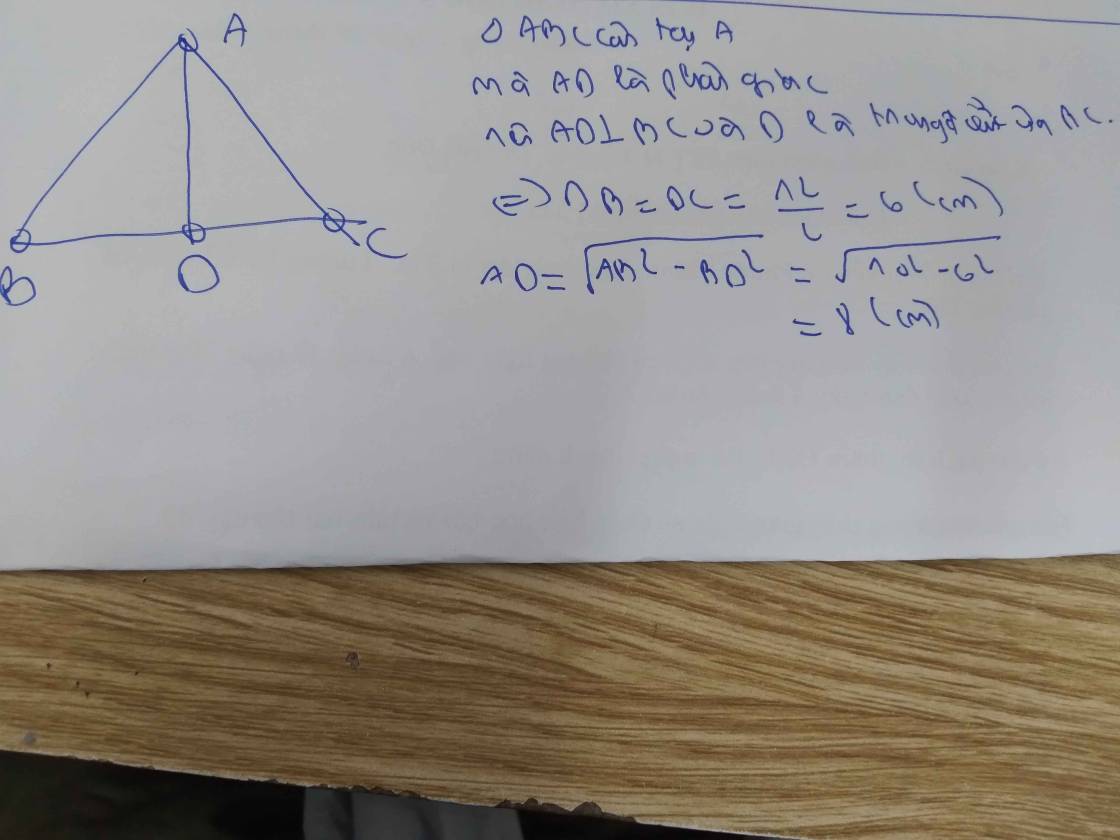
\(AM=MC=5cm\)
AC=8cm
\(S=\dfrac{4\cdot3}{2}=6\left(cm^2\right)\)
13 tháng 2 2022
a, Nửa chu vi là \(\frac{6+6+6}{2}=9cm\)
Diện tích tam giác là \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{9\left(9-6\right)\left(9-6\right)\left(9-6\right)}\)
\(=\sqrt{9.3.3.3}=9\sqrt{3}\)cm2
b, Xét tam giác ABC vuông tại A
tan^B = \(\frac{AC}{AB}\Rightarrow\frac{\sqrt{3}}{3}=\frac{2}{AB}\Rightarrow AB=\frac{6\sqrt{3}}{3}=2\sqrt{3}\)cm
Diện tích tam giác là \(\frac{1}{2}AB.AC=6\sqrt{3}\)cm2
c, Dựng AH là đường cao đồng thời là đường trung tuyến do tam giác ABC cân tại A
=> HC = BC/2 = 3 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AH=\sqrt{AC^2-HC^2}=4cm\)
Diện tích tam giác ABC là : \(\frac{1}{2}AH.BC=\frac{4.6}{2}=12cm^2\)
23 tháng 4 2023
a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm
HH
9 tháng 7 2020
1)
A B H D c m n
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)