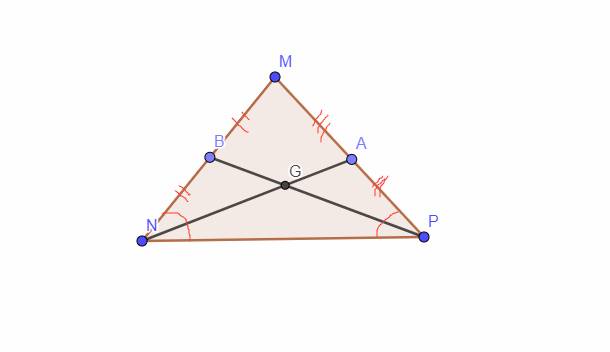
cho tam giác MNP có 2 đường trung tuyến NA;PB và cắt nhau tại G.Chứng minh rằng tam giác MNP cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 3 2023
`\color{blue}\text {#DuyNam}`
`NA` là đường trung tuyến
`-> A` là trung điểm của `MP`
`-> MA =AP`
`PB` là đường trung tuyến
`-> B` là trung điểm của `MN`
`-> MB=BN`
Vì Tam giác `MNP` cân tại `M`
`-> MN=MP,`\(\widehat{N}=\widehat{P}\)
`-> MB=MA=BN=AP`
Xét Tam giác `NAP` và Tam giác `PBN:`
`BN = AP`
\(\widehat{N}=\widehat{P}\)
`NP` chung
`=>` Tam giác `NAP =` Tam giác `PBN (c-g-c)`
`-> NA=PB (2` cạnh tương ứng `)`
17 tháng 2 2023
a: Xét ΔMEN và ΔMFP co
ME=MF
góc M chung
MN=NP
=>ΔMEN=ΔMFP
=>EN=FP
b: Xét ΔFNP và ΔEPN có
FN=EP
NP chung
FP=EN
=>ΔFNP=ΔEPN
=>góc ONP=góc OPN
=>ON=OP
Xét ΔMON và ΔMOP có
MO chung
ON=OP
MN=MP
=>ΔMON=ΔMOP
=>góc NMO=góc PMO
=>MO là phân giác của góc NMP
13 tháng 8 2016
Qua A kẻ đường thẳng // với MK cắt NP tại H => AH // MK
Do NA là trung tuyến => MA = PA ; I là trung điểm của NA
Xét tam giác PMK có : AH // MK; AM = PA => AH là đương trung bình của tam giác PMK => HP = HK (1)
Xét tam giác NAH có : IK // AH ; IN = IA => IK là đường trung bình của tam giác NAH => NK = HK (2)
Từ (1) và (2), suy ra : HP = HK= NK => NK = 1/2 KP
TT
15 tháng 1 2017
đường trung tuyến là đường đi qua trung điểm của đoạn thẳng đó
A B C M P N
tam giác ABC đều có 3 đường trung tuyến AM;BN;Cp suy ra các đoạn AP=PB=BM=MC=CN=NA
XÉT tam giác PMB và tam giác NMC có
PB = NC (cmt)
góc B = góc C (tam giác cân )
BM = Mc (cmt )
do đó tam giác PMB = tam giác NMC (c.g.c)
suy ra PM = MN (2 cạnh tương ứng )
xét tam giác PMB và tam giác PNA có
PA = PB (cmt)
BM = AN (cmt )
góc A = góc B (tam giác cân )
do đó tam giác PMB = tam giác PNA (c.g.c)
suy ra PN = PM (2 cạnh tuuwng ứng )
mà PM = MN suy ra PN = NM = MP
vậy tam giác MNP là tam giác cân\
`\color{blue}\text {#DuyNam}`
`NA, PB` là đường trung tuyến, cắt nhau tại `G`
`-> G` là trọng tâm của Tam giác `MNP`
`-> GN= 2/3 NA`
`-> GP=2/3 PB`
`NA=PB -> GN = GP`
Xét Tam giác `GNP: GN = GP`
`->` Tam giác `GNP` cân tại `G`.
`->` \(\widehat{N_1}=\widehat{P_1}\)
Xét Tam giác `NBP` và Tam giác `PAN:`
`NA = PB`
\(\widehat{N_1}=\widehat{P_1}\)
`NP` chung
`=>` Tam giác `NBP =` Tam giác `PAN (c-g-c)`
`=> BN = AP (2` cạnh tương ứng `)`
`-> 1/2 MN = 1/2 MP`
`-> MN = MP`
`->` Tam giác `MNP` cân tại `M`.