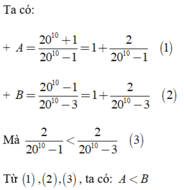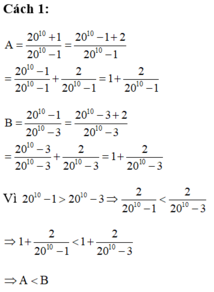So sánh :
A= 2010 + 1
2010 - 1
B = 2010 - 1
2010 - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(A=\dfrac{2010^{2011}+1}{2010^{2012}+1}\)
\(A< \dfrac{2010^{2011}+1+2009}{2010^{2012}+1+2009}\)
\(A< \dfrac{2010^{2011}+2010}{2010^{2012}+2010}\)
\(A< \dfrac{2010\left(2010^{2010}+1\right)}{2010\left(2010^{2011}+1\right)}\)
\(A< \dfrac{2010^{2010}+1}{2010^{2011}+1}\)
Mà \(B=\dfrac{2010^{2010}+1}{2010^{2011}+1}\)
\(\Rightarrow A< B\)

thì mới nói nếu dấu chia trừ mũ là xong
ý mà không được vậy mũ ra âm 1 à
ồ được bằng 1/2010

Ta có:
2010.A=\(\frac{2010^{2012}+2010}{2010^{2012}+1}\)
2010.B=\(\frac{2010^{2011}+2010}{2010^{2011}+1}\)
2010.A có phần thừa với 1 là:\(\frac{2009}{2010^{2012}+1}\)
2010.B có phần thừa với 1 là:\(\frac{2009}{2010^{2011}+1}\)
Vì \(\frac{2009}{2010^{2012}+1}<\frac{2009}{2010^{2011}+1}\)
=>2010.A<2010.B
=>A<B

Đổi ra hỗn số ta được
A = 20 10 + 1 20 10 − 1 = 20 10 − 1 + 2 20 10 − 1 = 1 + 2 20 10 − 1 ; B = 20 10 − 1 20 10 − 3 = 20 10 − 3 + 2 20 10 − 3 = 1 + 2 20 10 − 3 .
Vì 20 10 − 1 > 20 10 − 3 ⇒ 2 20 10 − 1 < 2 20 10 − 3 ⇒ A < B (so sánh hai phân số cùng tử).

A =\(\frac{2010^{2008}+1}{2010^{2009}+1}\)\(\Rightarrow2010A=\frac{2010^{2009}+2010}{2010^{2009}+1}=1+\frac{2009}{2010^{2009}+1}\)
\(B=\frac{2010^{2007}+1}{2010^{2008}+1}\Rightarrow2010B=\frac{2010^{2008}+2010}{2010^{2008}+1}=1+\frac{2009}{2010^{2008}+1}\)
Vì 2009 = 2009( tử số bằng nhau); \(2010^{2009}+1>2010^{2008}+1\)( mẫu số của A>B)
=> \(\frac{2010^{2008}+1}{2010^{2009}+1}< \frac{2010^{2007}+1}{2010^{2008}+1}\)
so sánh : cho A\(\frac{2010^{2011}+1}{2010^{2012}+1}\)
cho B =\(\frac{2010^{2010}+1}{2010^{2011}+1}\)

Ta có:
\(A=\frac{2010^{2011}+1}{2010^{2012}+1}\)
\(2010A=\frac{2010^{2012}+2010}{2010^{2012}+1}\)
\(2010A=1+\frac{2009}{2010^{2012}+1}\)
Lại có:
\(B=\frac{2010^{2010}+1}{2010^{2011}+1}\)
\(2010B=\frac{2010^{2011}+2010}{2010^{2011}+1}\)
\(2010B=1+\frac{2009}{2010^{2011}+1}\)
Vì \(1+\frac{2009}{2010^{2012}+1}< 1+\frac{2009}{2010^{2011}+1}\)
nên 2010A < 2010B
hay A < B
Vậy A < B