Chứng minh (3636 _ 910) chia hết cho 45
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sơ đồ con đường |
Lời giải chi tiết |
Áp dụng tính chất chia hết của một hiệu. |
Ta có: 36 ⋮ 9 ⇒ 36 36 ⋮ 9 9 ⋮ 9 ⇒ 9 10 ⋮ 9 ⇒ 36 36 + 9 10 ⋮ 9 |

1)
a) 3636-(12x-9)=36
12x-9=3636-36
12x-9=3600
12x=3600+9
12x=3609
x=3609:12
x=\(30\dfrac{3}{40}\)
1)
b) \(\left(\dfrac{x}{23}+45\right).67=8911\)
\(\dfrac{x}{23}+45=8911:67\)
\(\dfrac{x}{23}+45=133\)
\(x:23=133-45\)
\(x:23=88\)
\(x=88.23\)
\(x=2024\)

Đây bản chất là bài tìm ước của 3636 thôi em nhé. em viết số 3636 dưới dạng tích các thừa số nguyên tố là tìm được :
3636 = 22 . 32 . 101
Ư( 3636) = { 1; 2; 3; 4; 6; 9; 12; 18; 36; 101; 202; 303; 404; 606; 909; 1212; 1818; 3636}
Kết luận vậy 3636 chia hết cho các số :
1; 2; 3; 4; 6; 9; 12; 18; 36; 101; 202; 303; 404; 606; 909; 1212; 1818; 3636


a)vì 60.n chia hết cho 15
45 chia hết cho 15
=>60.n+45 chia hết cho 15
b)vì 60.n chia hết cho 30
45 ko chia hết cho 30
=>60.n +45 ko chia hết cho 30


Ta có: 60n + 45 chia hết cho 15 (với n thuộc N)
Vì 60n chia hết cho 15 và 45 chia hết cho 15
Ta có: 60n + 45 ko chia hết cho 30 (với n thuộc N)
Vì 60n chia hết cho 30 còn 45 ko chia hết cho 30

a)
\(3^{21}-3^{18}\\ =3^{17}.\left(3^4-3\right)\\ =3^{17}.\left(81-3\right)\\ =3^{17}.78\)
Vì \(3^{17}.78⋮78\) nên \(3^{21}-3^{18}⋮78\) (đpcm)
Vậy...
b)
\(81^7-27^9-9^{13}\\
=\left(3^4\right)^7-\left(3^3\right)^9-\left(3^2\right)^{13}\\
=3^{28}-3^{27}-3^{26}\\
=3^{24}.\left(3^4-3^3-3^2\right)\\
=3^{24}.\left(81-27-9\right)\\
=3^{24}.45\)
Vì \(3^{24}.45⋮45\) nên \(81^7-27^9-9^{13}⋮45\) (đpcm)
Vậy...
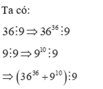
Ta có : \(36^{36}=\left(4.9\right)^{36}=4^{36}.9^{36}⋮9\)(1)
\(9^{10}⋮9\)(2)
Từ (1); (2) => \(36^{36}-9^{10}⋮9\) (3)
Ta có : \(36^{36}=\left(6^2\right)^{36}=6^{72}=\overline{.....6}\)
\(9^{10}=\overline{......1}\)
\(\Rightarrow36^{36}-9^{10}=\overline{......6}-\overline{......1}=\overline{......5}⋮5\) (4)
Từ (3) ; (4) \(\Rightarrow36^{36}-9^{10}⋮5;9\) Mà \(\left(5;9\right)=1\) \(\Rightarrow36^{36}-9^{10}⋮45\) (đpcm)