Giải phương trình: \(2x^2-11x+19=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LY
1
R
0
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Bình phương hai vế của phương trình đã cho, ta được:
\(\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\)
\( \Rightarrow x = \frac{5}{3}\) hoặc \(x = \frac{4}{7}\)
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)
TN
1
25 tháng 2 2018
Có |x-1| + |2x-3| + |3x+5|+|4x-7|+11x-8 = 0 (1)
<=> |x-1|+|2x-3|+|3x-5|+|4x-7| = 8-11x
Có \(\left|x-1\right|\ge0;\left|2x-3\right|\ge0;\left|3x-5\right|\ge0;\left|4x-7\right|\ge0\)
\(\Rightarrow\left|x-1\right|+\left|2x-3\right|+\left|3x-5\right|+\left|4x-7\right|\ge0\)
\(\Rightarrow8-11x\ge0\Leftrightarrow x\le\frac{8}{11}\)
\(\Rightarrow x-1< 0;2x-3< 0;3x-5< 0;4x-7< 0\)
=>\(\Rightarrow\hept{\begin{cases}\left|x-1\right|=1-x;\left|2x-3\right|=3-2x\\\left|3x-5\right|=5-3x;\left|4x-7\right|=7-4x\end{cases}}\)
Thay vào (1) có :
\(1-x+3-2x+5-3x+7-4x+11x-8=0\)
\(\Leftrightarrow x+8=0\Leftrightarrow x=-8\)( thỏa mãn điều kiện \(x\le\frac{8}{11}\))
Vậy x = - 8
Tích cho mk nhoa !!!! ~~
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau
Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
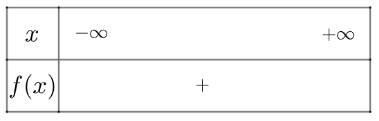
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là \(x = 5\)
2 tháng 3 2023
a: =>3x^2-3x-2x+2=0
=>(x-1)(3x-2)=0
=>x=2/3 hoặc x=1
b: =>2x^2=11
=>x^2=11/2
=>\(x=\pm\dfrac{\sqrt{22}}{2}\)
c: Δ=5^2-4*1*7=25-28=-3<0
=>PTVN
f: =>6x^4-6x^2-x^2+1=0
=>(x^2-1)(6x^2-1)=0
=>x^2=1 hoặc x^2=1/6
=>\(\left[{}\begin{matrix}x=\pm1\\x=\pm\dfrac{\sqrt{6}}{6}\end{matrix}\right.\)
d: =>(5-2x)(5+2x)=0
=>x=5/2 hoặc x=-5/2
e: =>4x^2+4x+1=x^2-x+9 và x>=-1/2
=>3x^2+5x-8=0 và x>=-1/2
=>3x^2+8x-3x-8=0 và x>=-1/2
=>(3x+8)(x-1)=0 và x>=-1/2
=>x=1
14 tháng 4 2021
c) \(\dfrac{x}{x-2}+\dfrac{x}{x+2}=\dfrac{4x}{x^2-4}.ĐKXĐ:x\ne2;-2\)
<=>\(\dfrac{x\left(x+2\right)}{x^2-4}+\dfrac{x\left(x-2\right)}{x^2-4}=\dfrac{4x}{x^2-4}\)
<=>x2+2x+x2-2x=4x
<=>2x2-4x=0
<=>2x(x-2)=0
<=>\(\left[{}\begin{matrix}2x=0< =>x=0\\x-2=0< =>x=2\left(loại\right)\end{matrix}\right.\)
Vậy pt trên có nghiệm là S={0}
d) 11x-9=5x+3
<=>11x-5x=9+3
<=>6x=12
<=>x=2
Vậy pt trên có nghiệm là S={2}
e) (2x+3)(3x-4) =0
<=> \(\left[{}\begin{matrix}2x+3=0< =>x=\dfrac{-3}{2}\\3x-4=0< =>x=\dfrac{4}{3}\end{matrix}\right.\)
Vậy pt trên có tập nghiệm là S={\(\dfrac{-3}{2};\dfrac{4}{3}\)}
14 tháng 4 2021
a) 5x+9 =2x
<=> 5x-2x=9
<=> 3x=9
<=> x=3
Vậy pt trên có nghiệm là S={3}
b) (x+1)(4x-3)=(2x+5)(x+1)
<=> (x+1)(4x-3)-(2x+5)(x+1)=0
<=>(x+1)(2x-8)=0
<=>\(\left[{}\begin{matrix}x+1=0< =>x=-1\\2x-8=0< =>2x=8< =>x=4\end{matrix}\right.\)
Vậy pt trên có tập nghiệm là S={-1;4}
NT
4
18 tháng 5 2016
Tập xác định : D=R. Phương trình đã cho tương đương với :
\(\frac{1}{8}\left(4x-4\right)^2-\frac{7}{4}\left(4x-4\right)+12-3\sqrt[3]{4x-4}=0\) (1)
Đặt \(t=\sqrt[3]{4x-4}\) thay vào phương trình (1) ta có :
\(t^6-14t^3-24t+96=0\)
hay :
\(\left(t-2\right)^2\left(t^4+4t^3+12t^2+18t+24\right)=0\) (2)
Nếu \(t\le0\) thì \(t^6-14t^3-24t+96>0\)
Nếu t > 0 thì \(t^4+4t^3+12t^2+18t+24>0\)
Do đó (2) <=> \(t=2\Rightarrow x=3\)
NT
0
\(2x^2-11x+19=0\Leftrightarrow2\left(x^2-\frac{11}{2}x+\frac{19}{2}\right)=0\Leftrightarrow x^2-\frac{11}{2}x+\frac{19}{2}=0\)
\(x^2-2.\frac{11}{4}.x+\frac{121}{16}+\frac{31}{16}=0\Leftrightarrow\left(x-\frac{11}{4}\right)^2+\frac{31}{16}=0\)
Vì \(\left(x-\frac{11}{4}\right)^2\ge0\forall x\Rightarrow\left(x-\frac{11}{4}\right)^2+\frac{31}{16}\ge\frac{31}{16}>0\forall x\)
Vậy phương trình vô nghiệm