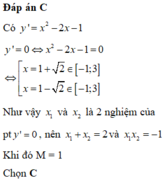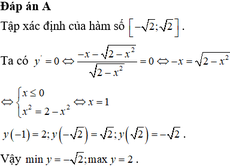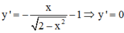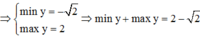giá trị lớn nhất của (x+2) : (x2+2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NB
1
5 tháng 1 2020
Ta có: \(\frac{9x^2-12x+4}{x^2-2x+2}\)
= \(\frac{9\left(x^2-2x+2\right)+6x-14}{x^2-2x+2}\)
= \(9+\frac{6x-14}{x^2-2x+2}\)
= \(9+\frac{x^2-2x+2-\left(x^2-8x+16\right)}{\left(x^2-2x+1\right)+1}\)
= \(9+1-\frac{\left(x-4\right)^2}{\left(x-1\right)^2+1}\)
= \(10-\frac{\left(x-4\right)^2}{\left(x-1\right)^2+1}\le10\forall x\)
Dấu "=" xảy ra <=> x - 4 = 0 <=> x = 4
Vậy Max của \(\frac{9x^2-12x+4}{x^2-2x+2}\)= 10 khi x = 4
NB
0
9 tháng 7 2021
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
9 tháng 7 2021
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
CM
16 tháng 7 2018
f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
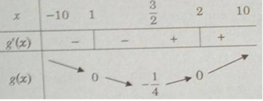
Vì
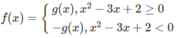
nên ta có đồ thị f(x) như sau:
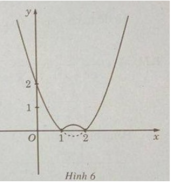
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132