giải phương trình (x^2+2x+64)(x^2+2x+27)=2010
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 11 2017
Đặt \(t=x^2+2x+27\left(t>0\right)\)
phương trình trở thành
\(t\left(t+37\right)=2010\Leftrightarrow t^2+37t-2010=0\)
\(\Leftrightarrow\left(t+67\right)\left(t-30\right)=0\)
\(\Rightarrow t=30\Rightarrow x^2+2x+27=30\Rightarrow x^2+2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
HR
27 tháng 11 2017
Đặt: \(x^2+2x+27=a\)
\(\Rightarrow\left(a+37\right)a=2010\)
\(\Leftrightarrow a^2+37a-2010=0\)
\(\Leftrightarrow\left(a-30\right)\left(a+67\right)=0\)
+) \(a=30\)
\(\Rightarrow x^2+2x+27=30\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=0\)
\(\Leftrightarrow x=\left[{}\begin{matrix}1\\-3\end{matrix}\right.\)
+) \(a=-67\)
\(\Rightarrow x^2+2x+27=-67\)
\(\Leftrightarrow x^2+2x+94=0\)(Vô nghiệm)
Vậy ..............
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
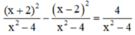
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
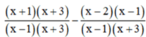
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
29 tháng 3 2016
Viết phương trình về dạng
\(\frac{2^x}{3^x+4^x}-\frac{4^x}{9^x+16^x}=\frac{-5}{2x}\) hay \(\frac{2^x}{3^x+4^x}+\frac{5}{x}=\frac{2^{2x}}{3^{2x}+4^{2x}}+\frac{5}{2x}\)
Xét hàm số \(f\left(t\right)=\frac{2^t}{3^t+4^t}+\frac{5}{t}\) luôn đồng biến
Đáp số : Phương trình vô nghiệm
22 tháng 4 2020
Bài 1 :
Ta có :
\(\frac{x+2011}{2013}+\frac{x+2012}{2012}=\frac{x+2010}{2014}+\frac{x+2013}{2011}\)
\(\Rightarrow\left(\frac{x+2011}{2013}+1\right)+\left(\frac{x+2012}{2012}+1\right)=\left(\frac{x+2010}{2014}+1\right)\)
\(+\left(\frac{x+2013}{2011}+1\right)\)
\(\Rightarrow\frac{x+4024}{2013}+\frac{x+4024}{2012}=\frac{x+4024}{2014}+\frac{x+4024}{2011}\)
\(\Rightarrow\frac{x+4024}{2013}+\frac{x+4024}{2012}-\frac{x+4024}{2014}-\frac{x+4024}{2011}=0\)
\(\Rightarrow\left(x+4024\right)\left(\frac{1}{2013}+\frac{1}{2012}-\frac{1}{2014}-\frac{1}{2011}\right)=0\)
\(\Rightarrow x+4024=0\)
\(\Rightarrow x=-4024\)
22 tháng 4 2020
Bài 2 :
Đặt \(x^2+2x+1=a\Rightarrow a=\left(x+1\right)^2\ge0\)
=> Phương trình trở thành
\(\frac{a}{a+1}+\frac{a+1}{a+2}=\frac{7}{6}\)
\(\Rightarrow\frac{a}{a+1}.6\left(a+1\right)\left(a+2\right)+\frac{a+1}{a+2}.6\left(a+1\right)\left(a+2\right)=\frac{7}{6}.6\left(a+1\right)\left(a+2\right)\)
\(\Rightarrow6a\left(a+2\right)+6\left(a+1\right)^2=7\left(a+1\right)\left(a+2\right)\)
\(\Rightarrow12a^2+24a+6=7a^2+21a+14\)
\(\Rightarrow5a^2+3a-8=0\)
\(\Rightarrow\left(a-1\right)\left(5a+8\right)=0\)
Vì \(a\ge0\Rightarrow a=1\)
\(\Rightarrow x^2+2x+1=1\)
\(x^2+2x=0\)
\(\Rightarrow x\left(x+2\right)=0\)
\(\Rightarrow x\in\left\{-2,0\right\}\)
29 tháng 7 2019
\(\frac{x^2-4x}{x^2+4x}+\frac{27}{2x^2+7x-4}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\frac{x\left(x-4x\right)}{x\left(x+4x\right)}+\frac{27}{2x^2+7x-4}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\frac{x\left(x-4\right)}{x\left(x+4\right)}+\frac{27}{2x^2+8x-x-4}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\frac{x\left(x-4\right)}{x\left(x+4\right)}+\frac{27}{2x\left(x+4\right)-\left(x+4\right)}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\frac{x\left(x-4\right)}{x\left(x+4\right)}+\frac{27}{\left(x+4\right)\left(2x-1\right)}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\frac{x-4}{x+4}+\frac{27}{\left(x+4\right)\left(2x-1\right)}=\frac{7-2x}{2x-1}-1\)
\(\Leftrightarrow\left(x-4\right)\left(2x-1\right)+27=\left(7-2x\right)\left(x+4\right)-\left(x+4\right)\left(2x-1\right)\)
\(\Leftrightarrow2x^4-9x+31=-8x+32-4x^2\)
\(\Leftrightarrow2x^2-9x+31+8x-32+4x^2=0\)
\(\Leftrightarrow6x^2-x-1=0\)
\(\Leftrightarrow6x^2+2x-3x-1=0\)
\(\Leftrightarrow2x\left(3x+1\right)-\left(3x+1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\2x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\left(\text{nhận}\right)\\x=\frac{1}{2}\left(\text{loại}\right)\end{cases}}\)
\(\Rightarrow x=-\frac{1}{3}\)
Vậy: nghiệm phương trình là \(-\frac{1}{3}\)
26 tháng 4 2022
????
xin lỗi nha !
mình mới học lớp 3
mà bài này khó nắm
BM
0
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(a,3^{x-1}=27\\ \Leftrightarrow3^{x-1}=3^3\\ \Leftrightarrow x-1=3\\ \Leftrightarrow x=4\\ b,100^{2x^2-3}=0,1^{2x^2-18}\\ \Leftrightarrow10^{4x^2-6}=10^{-2x^2+18}\\ \Leftrightarrow4x^2-6=-2x^2+18\\ \Leftrightarrow6x^2=24\\ \Leftrightarrow x^2=4\\ \Leftrightarrow x=\pm2\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(c,\sqrt{3}e^{3x}=1\\ \Leftrightarrow e^{3x}=\dfrac{1}{\sqrt{3}}\\ \Leftrightarrow3x=ln\left(\dfrac{1}{\sqrt{3}}\right)\\ \Leftrightarrow x=\dfrac{1}{3}ln\left(\dfrac{1}{\sqrt{3}}\right)\)
\(d,5^x=3^{2x-1}\\ \Leftrightarrow2x-1=log_35^x\\ \Leftrightarrow2x-1-xlog_35=0\\ \Leftrightarrow x\left(2-log_35\right)=1\\ \Leftrightarrow x=\dfrac{1}{2-log_35}\)
x=1 hoặc x= -3
Nhập vào máy tính Casio fx-570VN plus:
(X2+2X+64)(X2+2X+27) ALPHA = 2010 Shift Solve = Kq là 1