 giải hết mấy câu này hộ t với
giải hết mấy câu này hộ t với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,\dfrac{5}{8}\times3=\dfrac{15}{8}\)
\(c,5\times\dfrac{6}{21}=\dfrac{30}{21}\)
\(d,\dfrac{3}{5}\times\dfrac{4}{5}\times\dfrac{6}{7}=\dfrac{72}{175}\)

c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)


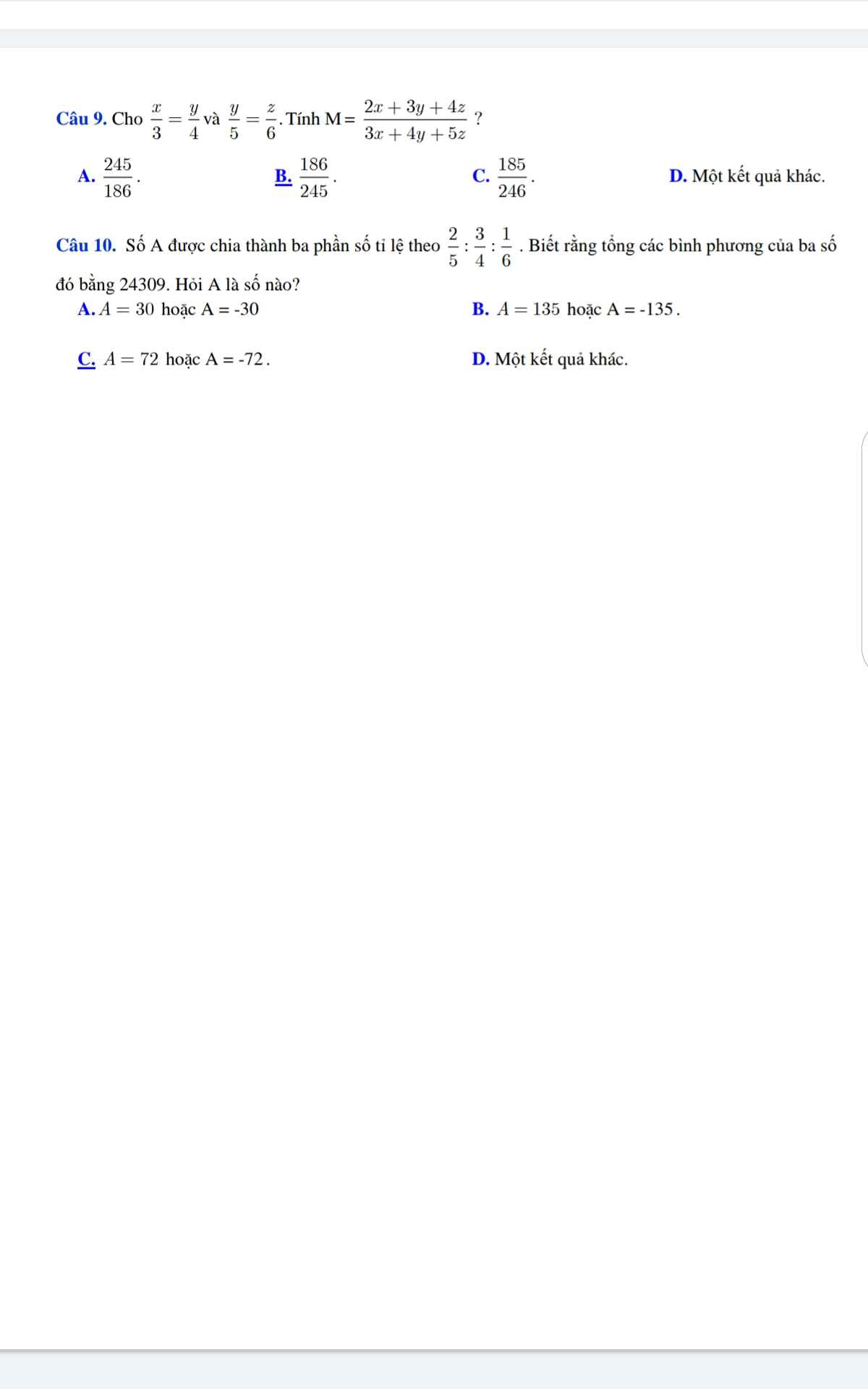
Câu 9 cần bs điều kiện $x,y,z\neq 0$
$\frac{x}{3}=\frac{y}{4}\Rightarrow \frac{x}{15}=\frac{y}{20}$
$\frac{y}{5}=\frac{z}{6}\Rightarrow \frac{y}{20}=\frac{z}{24}$
$\Rightarrow \frac{x}{15}=\frac{y}{20}=\frac{z}{24}$ và đặt $=t$ (đk: $t\neq 0$)
$\Rightarrow x=15t; y=20t; z=24t$
Khi đó:
$M=\frac{2.15t+3.20t+4.24t}{3.15t+4.20t+5.24t}=\frac{186t}{245t}=\frac{186}{245}$
Đáp án B.
Câu 10:
Giả sử số $A$ được chia thành 3 phần $a,b,c$ sao cho
$a:b:c=\frac{2}{5}: \frac{3}{4}: \frac{1}{6}$
Đặt $a=\frac{2}{5}t; b=\frac{3}{4}t; c=\frac{1}{6}t$
$A=a+b+c=\frac{2}{5}t+\frac{3}{4}t+\frac{1}{6}t=\frac{79}{60}t$
Có:
$a^2+b^2+c^2=(\frac{2}{5}t)^2+(\frac{3}{4}t)^2+(\frac{1}{6}t)^2=24309$
$t^2=32400$
$t=\pm 180$
$\Rightarrow A=\frac{79}{60}t=\frac{79}{60}\pm 180=\pm 237$
Đáp án D.

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

4n + 3 chia hết cho 2n + 1
4n + 2 + 1 chia hết cho 2n + 1
2.(2n + 1) + 1 chia hết cho 2n + 1
=> 1 chia hết cho 2n + 1
=> 2n + 1 thuộc Ư(1) = {1 ; -1}
Ta có bảng sau :
| 2n + 1 | 1 | -1 |
| n | 0 | -2 |







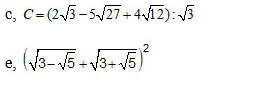
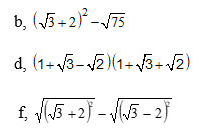 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp

 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
