bài 1: biểu diễn tập hợp C gồm các số tự nhiên có 3 chữ số khác nhau tạo nên từ 1,2,3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 7 2017
Chọn D
Gọi số tự nhiên có chữ số khác nhau lấy từ các phần tử của tập A là 
+) Chọn a có 6 cách.
+) Chọn bốn chữ số b,c,d,e có A 6 4 cách.
Vậy số cách lập số tự nhiên có 5 chữ số khác nhau lấy từ các phần tử của tập A là
6.
A
6
4
= 2160 cách. Do đó số phần tử của không gian mẫu là 
Gọi biến cố B: ‘‘Số tự nhiên lập được chia hết cho 5 và các chữ số 1,2,3 luôn có mặt cạnh nhau’’.
TH1: Số lập được có dạng a b c d 0 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn 1 số trong tập 
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .3 P 2 = 36 số.
TH2: Số lập được có dạng a b c 05 ¯
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta có P 3 cách chọn số a,b,c
Vậy có P 3 = 6 số.
TH3: Số lập được có dạng 
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có P 3 cách.
+) Chọn số trong tập {4;6} có C 2 1 = 2 cách.
+) Xếp khối X và số vừa chọn vào vị trí có P 2 cách.
Theo quy tắc nhân ta có P 3 .2 P 2 = 24 số.
Vậy số kết quả xảy ra của biến cố B là 
Xác suất của biến cố B là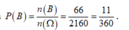 
23 tháng 9 2017
bài 1
a 102,120,201,210
b [1],[2],[3],[1;2],[2;3],[1;3],[1;2;3],[]
TY
23 tháng 9 2017
a) A=(120;102;210;201)
b) (120)c A;(102) c A;(210) c A;(201) c A.
14 tháng 7 2016
a) A = { 230;203;320;302 }
Tập hợp con của A là :
{230} ; {203} ; {320} ; {302} ; {230;203} ; {203;320} ; {320;302} ; {230;320} {230;320} {230;302} ; {203;302} {230;203;320} ; {230;320;302} ; {203;320;302} ; {230;204;320;302};\(\varnothing\)
14 tháng 7 2016
a) Viết tập hợp A các số tự nhiên gồm 3 chữ số khác nhau tạo thành tưd 3 chữ số trên
\(A=\left\{230;203;320;302\right\}\)
b) Viết các tập hợp con của A
\(\left\{230\right\};\left\{203\right\};\left\{320\right\};\left\{302\right\};\left\{230;203\right\};\left\{230;320\right\};\left\{230;302\right\};\left\{203;320\right\};\left\{203;302;\right\}\) \(\left\{320;302\right\};\left\{230;203;320\right\};\left\{230;203;302\right\};\left\{203;320;302\right\};\left\{230;320;302\right\}\) \(\left\{230;203;320;302\right\};\left\{\varnothing\right\}\)
:C={123,132,213,231,321,312}