Cho góc xAy=60 độ và điểm B nằm trên tia Ax sao cho AB=3cm.Tính bán kính đường tròn (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


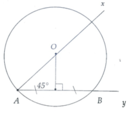
a, Dựng đường thẳng d là trung trực của AB, d cắt tia Ay tại O suy ra (O;OA) là đường tròn cần dựng.
HS tự chứng minh
b, Tính được: OA = 3 2 3 cm

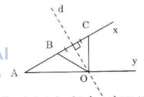
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.

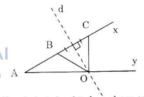
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.

1: Vì O là trung điểm của AB
nên \(OA=OB=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Do đó: A,B đều nằm trên đường tròn (O;3cm)
2:
a) Ta có: \(\widehat{AOx}+\widehat{BOx}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{BOx}+60^0=180^0\)
hay \(\widehat{BOx}=120^0\)