Cho hình bên;
a,Kể tên các góc so le trong
b,Kể tên các góc đồng vị
c,Kể tên các góc trong cùng phía
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
1
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Hình chóp tứ giác đều \(S.MNPQ\) có:
a) Mặt bên: \(SMN\); \(SNP\); \(SPQ\); \(SMQ\)
Mặt đáy: \(MNPQ\)
b) Các cạnh bên bằng nhau: \(SM = SN = SP = SQ = 15\)cm
Các cạnh đáy bằng nhau: \(MN = NP = PQ = MQ = 8\)cm
CM
1 tháng 8 2017
Các giao điểm trên hình: A, B, C, D, E, F, G, H, I, J (hình 19a)
PT
Cho hình bên. Tính diện tích hình ABCDE. Biết rằng AB và EC song song và có kích thước như hình bên.
2
CM
28 tháng 5 2018
Diện tích hình thang ABCE là: (17,5 + 7) x 7 : 2 = 85,75cm²
Diện tích hình tam giác DEC là: 17,5 x 7 : 2 = 61,25cm²
Diện tích ABCDE là: 85,75 + 61,25 = 147cm²
21 tháng 8 2023
a: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
b: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
c: Có 4 mặt bên là hình chữ nhật
d: Có tất cả là 6 mặt là hình chữ nhật
NB
29 tháng 1 2023
Ta có: 25=5x5
=> Cạnh hình vuông hay đường kính hình tròn là 5cm
=> bán kính hình tròn là
5:2=2,5(cm)
a/ diện tích hình tròn là
2,5x2,5x3,14=19,625(cm2)
b/Diện tích phần gạch chéo là:
25-19,625=5,375(cm2)
Đ/s:...
@Teoyewmay
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Hình chóp tam giác đều \(S.DEF\) có:
a) Mặt bên: \(SDE\); \(SDF\); \(SEF\)
Mặt đáy: \(DEF\)
b) Các cạnh bên bằng nhau: \(SE = SF = SD = 5\)cm
Các cạnh đáy bằng nhau: \(ED = EF = DF = 3\)cm
c) Đáy \(DEF\) là tam giác đều nên ba góc ở đáy bằng nhau và bằng \(60^\circ \)
28 tháng 3 2021
a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
28 tháng 3 2021
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm
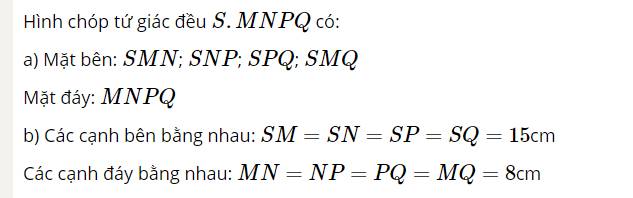
Đề bị lỗi hiển thị rồi. Bạn xem lại nhé.