cho hệ phương trình:3x+my =4 và x+y=1
Tìm m để hpt trên có nghiêm x<0,y>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2021
\(\left\{{}\begin{matrix}mx+y=m\\mx+m^2y=m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}mx+y=m\\\left(m^2-1\right)y=0\end{matrix}\right.\)
Hệ đã cho có nghiệm duy nhất \(\Leftrightarrow m^2-1\ne0\)
\(\Leftrightarrow m\ne\pm1\)
16 tháng 3 2020
1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)
30 tháng 3 2021
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=m+1-my\\m^2+m-m^2y+y=3m-1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=m+1-my\\y\left(m^2-1\right)=m^2-2m+1\end{matrix}\right.\)
Với m = 1 ta có: \(\left\{{}\begin{matrix}x=2-y\\0y=0\left(VSN\right)\end{matrix}\right.\)
\(\Rightarrow\) Hpt vô số nghiệm
Với m = -1 ta có: \(\left\{{}\begin{matrix}x=y\\0y=4\left(VN\right)\end{matrix}\right.\)
\(\Rightarrow\) Hpt vô nghiệm
Với m \(\ne\) \(\pm\)1 ta có: \(\left\{{}\begin{matrix}x=m+1-my\\y=\dfrac{m^2-2m+1}{m^2-1}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=m+1-\dfrac{m\left(m-1\right)^2}{\left(m-1\right)\left(m+1\right)}=m+1-\dfrac{m\left(m-1\right)}{m+1}=m+1-\dfrac{m^2-m}{m+1}\\y=\dfrac{m^2-2m+1}{m^2-1}=\dfrac{\left(m-1\right)^2}{\left(m-1\right)\left(m+1\right)}=\dfrac{m-1}{m+1}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=\dfrac{m^2+2m+1-m^2+m}{m+1}=\dfrac{3m+1}{m+1}\\y=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Vậy hpt có nghiệm duy nhất x = ..; y = ... với x \(\ne\) \(\pm\) 1
Ta có: x = |y|
\(\Leftrightarrow\) \(\dfrac{3m+1}{m+1}=\left|\dfrac{m-1}{m+1}\right|\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}\dfrac{3m+1}{m+1}=\dfrac{m-1}{m+1}\\\dfrac{3m+1}{m+1}=\dfrac{1-m}{m+1}\end{matrix}\right.\)
\(\Rightarrow\) \(\left[{}\begin{matrix}3m+1=m-1\\3m+1=1-m\end{matrix}\right.\) (Vì m \(\ne\) -1)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}2m=-2\\4m=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[{}\begin{matrix}m=-1\\m=0\end{matrix}\right.\)
Vì m \(\ne\) -1 nên m = -1 KTM
\(\Rightarrow\) m = 0 thỏa mãn đk
Vậy m = 0
Chúc bn học tốt!
PT
Cho hệ phương trình:
3 x + m y = 4 x + y = 1
b) Tìm m để hệ phương trình trên có nghiệm x < 0; y > 0
1
CM
25 tháng 4 2017
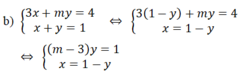
Với m - 3 ≠ 0 ⇔ m ≠ 3 hệ phương trình có nghiệm:
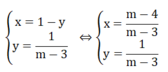
Vì nghiệm của hệ phương trình thỏa mãn x < 0; y > 0 nên ta có:
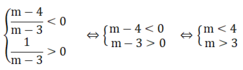
Vậy với điều kiện 3 < m < 4 thì hệ phương trình có nghiệm thỏa mãn x < 0; y > 0
23 tháng 1 2021
a) Thay \(m=1\) vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}3x-y=1\\x+2y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy ...
b) HPT \(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\y=2m-1-3x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=-m-1\end{matrix}\right.\)
Ta có: \(x^2+y^2=5\)
\(\Rightarrow m^2+m^2+2m+1=5\) \(\Leftrightarrow m^2+m-2=0\) \(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Vậy ...
c) Hệ phương trình luôn có nghiệm duy nhất
Ta có: \(x-3y>0\)
\(\Rightarrow m-3\left(-m-1\right)>0\)
\(\Leftrightarrow4m+3>0\) \(\Leftrightarrow m>-\dfrac{3}{4}\)
Vậy ...