Tìm x, y ϵ N biết: (x-1)(2y - 1)=10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy (x+1)(2y-5)=143=11.13=13.11=143.1=1.143
Suy ra ta có 4 trường hợp sau:
-Nếu x+1=11suy ra x=10 ; 2y-5=13 suy ra y=9
-Nếu x+1=13 suy ra x=12 ; 2y-5=11 suy ra y=8
-Nếu x+1=143 suy ra x=142 ; 2y-5=1 suy ra y=3
-Nếu x+1=1 suy ra x=0 ; 2y-5=143 suy ra y=74
Vậy x=10 thì y=9
x=12 thì y=8
x=142 thì y=3
x=0 thì y=74

Lời giải:
$\frac{1}{x}+\frac{1}{y}=\frac{1}{8}$
$\Rightarrow \frac{x+y}{xy}=\frac{1}{8}$
$\Rightarrow 8(x+y)=xy$
$\Rightarrow xy-8x-8y=0$
$\Rightarrow x(y-8)-8(y-8)=64$
$\Rightarrow (x-8)(y-8)=64$
Do $x,y$ tự nhiên nên $x-8,y-8\in\mathbb{Z}$
$\Rightarrow x-8$ là ước của $64$. Mà $x-8>-8$ với mọi $x\in\mathbb{N}^*$ nên:
$x-8\in\left\{1; 2; 4; 8; 16; 32; 64; -1; -2; -4\right\}$
Đến đây bạn chỉ cần chịu khó xét các TH là được.

a)(2x+1).(y-3)=10
có:10=1.10=2.5=10.1=5.2
xét:2x+1=1 ; y-3=10
2x=1-1=0 y=10+3=13(nhận)
x=0:2=0(nhận)
......(xét tiếp các trường hợp còn lại)
Vậy............
b)(3x-2).(2y-3)=1
\(\Leftrightarrow\) 3x-2=1 hoặc 2y-3=1
3x=1+2=3 2y=1+3=4
x=3:3=1 y=4:2=2
Vậy x=1 và y=2
c làm tương tự phần a

Bài 2:
a: =>x=0 hoặc x+3=0
=>x=0 hoặc x=-3
b: =>x-2=0 hoặc 5-x=0
=>x=2 hoặc x=5
c: =>x-1=0
hay x=1

Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: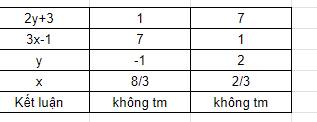
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.

Lời giải:
$3x-2y+6xy=1$
$\Rightarrow (3x+6xy)-(2y+1)=0$
$\Rightarrow 3x(1+2y)-(2y+1)=0$
$\Rightarrow (1+2y)(3x-1)=0$
$\Rightarrow 1+2y=0$ hoặc $3x-1=0$
$\Rightarrow y=\frac{-1}{2}$ hoặc $x=\frac{-1}{3}$ (vô lý vì $x,y$ là số nguyên)
Vậy không tồn tại $x,y$ thỏa mãn đề.

Bài 2:
a: =>x=0 hoặc x=-3
b: =>x-2=0 hoặc 5-x=0
=>x=2 hoặc x=5
c: =>x-1=0
hay x=1

1; 134. (-76) + 348.(-24) - 214.76
= (-76.) (134 + 214) + 348.(-24)
= -76. 348 + 348. (-24)
= - 348 .(76 + 24)
= - 348. 100
= - 34800
2; \(x\); y \(\in\) Z biết \(x\).(y + 1) - ( y + 1) = 10
(y + 1).(\(x\) - 1) = 10
10 = 2.5; Ư(10) = {- 10; - 5; -2; -1; 1; 2; 5; 10}
Lập bảng ta có:
| \(x\) - 1 | - 10 | - 5 | - 2 | -1 | 1 | 2 | 5 | 10 |
| \(x\) | -9 | -4 | -1 | 0 | 2 | 3 | 6 | 11 |
| y + 1 | -1 | -2 | -5 | -10 | 10 | 5 | 2 | 1 |
| y | - 2 | -3 | -6 | - 11 | 9 | 4 | 1 | 0 |
Theo bảng trên ta có các cặp \(x\); y nguyên thỏa mãn đề bài là:
(\(x\); y) = (-9; -2); (-4; - 3); (-1; -6); (0; -11); (2; 9); (3; 4); (6; 1); (11; 0)

\(3x+6xy+2y=7\)
\(\Leftrightarrow3x+6xy+1+2y=8\)
\(\Leftrightarrow3x\left(1+2y\right)+\left(1+2y\right)=8\)
\(\Leftrightarrow\left(3x+1\right)\left(1+2y\right)=8\)
Do \(1+2y\) luôn lẻ với y nguyên nên ta chỉ cần xét các cặp ước của 8 mà \(1+2y\) nhận giá trị lẻ là \(-1;1\)
| 1+2y | -1 | 1 |
| 3x+1 | -8 | 8 |
| y | -1 | 0 |
| x | -3 | 7/3(loại) |
Vậy \(\left(x;y\right)=\left(-3;-1\right)\) là nghiệm duy nhất
Lời giải:
Vì $x,y\in\mathbb{N}$ nên $x-1, 2y-1\in\mathbb{Z}$
Mà $(x-1)(2y-1)=10$ và $2y-1$ lẻ nên ta có các TH sau:
TH1:
$x-1=10; 2y-1=1\Rightarrow x=11; y=1$
TH2:
$x-1=-10; 2y-1=-1\Rightarrow x=-9; y=0$
TH3:
$x-1=2, 2y-1=5\Rightarrow x=3; y=3$
TH4:
$x-1=-2; 2y-1=-5\Rightarrow x=-1; y=-2$