Lớp 10A có 50 học sinh , trong đó có 13 học sinh thích môn Lý ; 20 học sinh thích môn Anh ; 18 học sinh thích ít nhất một trong hai môn . Hỏi có bao nhiêu học sinh thích cả hai môn ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MM
24 tháng 8 2019
Sơ đồ học sinh lớp 10A: 25 bạn 20 bạn 15 bạn 5 1 6 7
Số học sinh thích môn toán và tiếng anh và văn là:(25+15+20)-(5+7+1+6)=42(bạn)
Số học sinh không thích môn nào là:45-42=3(học sinh)
1 tháng 2 2021
eh8 ihgggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
7 tháng 11 2021
Số học sinh chỉ giỏi Toán là:
20-10=10(bạn)
Số học sinh chỉ giỏi Lý là:
20-10=10(bạn)
Số học sinh chỉ giỏi Hóa là:
45-10-10=25(bạn)
giúp em với ạ
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 8 2023
Số học sinh thích môn toán là: 50 \(\times\) \(\dfrac{20}{100}\) = 10 (học sinh)
Số học sinh thích môn anh văn là: 50 \(\times\) \(\dfrac{50}{100}\) = 25 (học sinh)
Đáp số:
CM
28 tháng 2 2019
Đáp án A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
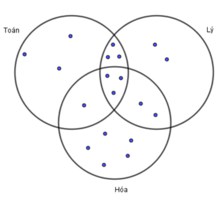
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: 6−3=3 (em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: 4−3=1 (em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: 5−3=2 (em)
Số học sinh chỉ giỏi một môn Toán là: 10−3−3−1=3 (em)
Số học sinh chỉ giỏi một môn Lý là: 10−3−3−2=2 (em)
Số học sinh chỉ giỏi một môn Hóa là: 11−1−3−2=5 (em)
Số học sinh giỏi ít nhất một trong ba môn là:
3+2+5+1+2+3+3=19 (em)
NM
Nguyễn Minh Quang
Giáo viên
9 tháng 11 2021
Gọi A,B,C là tập hợp các học sinh tích môn toán , Văn , Anh
ta có :
\(\hept{\begin{cases}\left|A\right|=10,\left|B\right|=20,\left|C\right|=25\\\left|A\cap B\cap C\right|=3\\\left|A\cup B\cup C\right|=40\end{cases}}\) ta có : \(\left|A\cup B\cup C\right|=\left|A\right|+\left|B\right|+\left|C\right|-\left(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|\right)+\left|A\cap B\cap C\right|\)
nên \(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|=18\)
Do đó số học sinh chỉ thích đúng hai môn là :
\(\left|A\cap B\right|+\left|B\cap C\right|+\left|C\cap A\right|-3\left|A\cap B\cap C\right|=18-3\times3=9\)
23 tháng 9 2021
\(a,\) Số học sinh chỉ giỏi Toán là: 7 – (3 – 1) – (4 – 1) – 1 = 1
Số học sinh chỉ giỏi Lý là: 5 – (3 – 1) – (2 – 1) – 1 = 1
Số học sinh chỉ giỏi Hóa là: 6 – (4 – 1) – (2 – 1) – 1 = 1
\(b,\) Số học sinh giỏi Lý, Toán không giỏi Hóa là: 3 – 1 = 2
Số học sinh giỏi Toán, Hóa không giỏi Lý là: 4 – 1 = 3
Số học sinh giỏi Lý, Hóa không giỏi Toán là: 2 – 1 = 1
Bạn xem lại đề nhé bạn. Tại sao có 20 học sinh thích môn Anh nhưng lại chỉ có 18 học sinh thích ít nhất 1 trong 2 môn vậy bạn?