Cho E = 1 + 4 + 41 + 42 + 43 + 44 + 45 + ................. + 499
Chứng minh rằng : a) E ⋮ 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PB
2
19 tháng 12 2021
\(S=\left(1+4\right)+\left(4^2+4^3\right)+...+\left(4^{98}+4^{99}\right)\\ S=\left(1+4\right)+4^2\left(1+4\right)+...+4^{98}\left(1+4\right)\\ S=\left(1+4\right)\left(1+4^2+...+4^{98}\right)=5\left(1+4^2+...+4^{98}\right)⋮5\)
19 tháng 12 2021
\(S=\left(1+4\right)+...+4^{98}\left(1+4\right)\)
\(=5\left(1+...+4^{98}\right)⋮5\)
MP
0
K
1
LV
2
20 tháng 7 2018
Ta có: \(\frac{1}{41}+\frac{1}{42}+\frac{1}{43}+...+\frac{1}{60}< \frac{1}{40}+\frac{1}{40}+...+\frac{1}{40}=\frac{1}{40}.20=\frac{1}{2}\)
\(\frac{1}{61}+\frac{1}{62}+\frac{1}{63}+...+\frac{1}{80}< \frac{1}{60}+\frac{1}{60}+\frac{1}{60}+...+\frac{1}{60}=\frac{1}{60}.20=\frac{1}{3}\)
\(\Rightarrow\frac{1}{41}+\frac{1}{42}+...+\frac{1}{80}< \frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{3+2}{6}=\frac{5}{6}\) (đpcm)
SN
2
SN
1
KV
7 tháng 7 2023
Số số hạng của tổng:
60 - 41 + 1 = 20
Ta có:
1/41 + 1/42 + 1/43 + ... + 1/60 > 1/60 + 1/60 + 1/60 + ... + 1/60 (20 số 1/60)
= 20/60
= 1/3
Vậy 1/41 + 1/42 + 1/43 + ... + 1/60 > 1/3
12 tháng 8 2023
a)\(...A=\dfrac{2^{50+1}-1}{2-1}=2^{51}-1\)
b) \(...\Rightarrow B=\dfrac{3^{80+1}-1}{3-1}=\dfrac{3^{81}-1}{2}\)
c) \(...\Rightarrow C+1=1+4+4^2+4^3+...+4^{49}\)
\(\Rightarrow C+1=\dfrac{4^{49+1}-1}{4-1}=\dfrac{4^{50}-1}{3}\)
\(\Rightarrow C=\dfrac{4^{50}-1}{3}-1=\dfrac{4^{50}-4}{3}=\dfrac{4\left(4^{49}-1\right)}{3}\)
Tương tự câu d,e,f bạn tự làm nhé
CM
15 tháng 5 2019
Chọn B
Do kích thước mẫu N = 18 là số chẵn nên số trung vị là trung bình cộng của 2 giá trị đứng ở vị trí thứ 9 và thứ 10
CM
2 tháng 10 2019
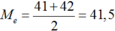
Chọn A.
Để tính số trung bình ta ghi lại số liệu theo bảng tần số:
Vậy số trung bình gần với số 42 nhất.
\(E=1+4+4+4^2+4^3+4^4+...+4^{99}\)
\(E=\left(1+4\right)+4\left(1+4\right)+4^3\left(1+4\right)+....+4^{98}\left(1+4\right)\)
\(E=5\left(1+4+4^3+.....+4^{98}\right)⋮5\)
S=(1+4)+(42+43)+...+(498+499)S=(1+4)+42(1+4)+...+498(1+4)S=(1+4)(1+42+...+498)=5(1+42+...+498)⋮5