Chứng minh AH là tia phân giác của góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 7 2021
O A m n y t 1 2 1 2 x 3 4
a) Ta có: Ot là tia phân giác của \(\widehat{xOy}\) => \(\widehat{O_1}=\widehat{O_2}=\frac{\widehat{xOy}}{2}\) (1)
On là tia phân giác của \(\widehat{xAm}\) => \(\widehat{A_1}=\widehat{A_2}=\frac{1}{2}\widehat{xAm}\) (2)
Mà Am // Oy (gt) => \(\widehat{xAm}=\widehat{xOy}\) (đồng vị) (3)
Từ (1), (2) và (3) => \(\widehat{O_1}=\widehat{O_2}=\widehat{A_1}=\widehat{A_2}\)
mà \(\widehat{A_2}\) và \(\widehat{O_2}\)ở vị trí đồng vị => An // Ot
b) Ta có: \(\hept{\begin{cases}AH\perp Ot\left(gt\right)\\Ot//On\left(cmt\right)\end{cases}}\Rightarrow AH\perp An\)
Xét tam giác OAH vuông tại H có: \(\widehat{O_2}+\widehat{A_3}=90^0\)
Lại có: \(\widehat{A_1}+\widehat{A_4}=90^0\)(phụ nhau)
mà \(\widehat{O_2}=\widehat{A_1}\) (cm câu a)
=> \(\widehat{A_3}=\widehat{A_4}\) -> AH là tia phân giác của \(\widehat{OAm}\)
TH
12 tháng 1 2018
A B m 2 1
Chú ý:Góc ngoài tam giác bằng tổng số đo 2 góc trog tam giác không kể với nó
Vậy góc(A1)+góc(A2)=góc(B)+góc(C) .(1)
Do Am là tia phân giác ngoài tại đỉnh A của tam giác ABC nên góc A1=góc (A2).(2)
Lại có tam giác ABC cân tại A do(AB=AC) nên góc (B)=góc(C).(3)
Từ(1);(2) và (3) =>góc(A1)+góc (A1)=góc (C)+góc(C)
Suy ra góc( A1)=góc(C) mà 2 góc này nằm ở vị ttrí so le nhau
Do đó Am//BC . (dpcm)
8 tháng 7 2023
a: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
=>góc C=góc BAH
b: góc CAD+góc BAD=90 độ
góc CDA+góc HAD=90 độ
mà góc BAD=góc HAD
nên góc CAD=góc CDA
c: ΔCAD cân tại C có CK là phân giác
nên CK vuông góc AD
29 tháng 6 2017
A O n x m t y 1 2 1 2
a) CMR: An // Ot
An là phân giác góc xAm (gt) => góc A1=góc A2=\(\frac{1}{2}\)góc xAm (1)
Ot là phân giác góc xOy (gt) => góc O1=góc O2=\(\frac{1}{2}\)góc xOy (2)
Am // Oy (gt) => góc xAm=góc AOy (đồng vị) (3)
Từ (1), (2) và (3) => góc A1=góc O1
Mà 2 góc này ở vị trí đồng vị
=> An // Ot (dpcm)
Câu b vì mình không biết AH ở đâu nên mình không làm được bạn nhé!
7 tháng 11 2021
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
DT
9 tháng 3 2022
Có gì khong hiểu hỏi lại cj nhé:
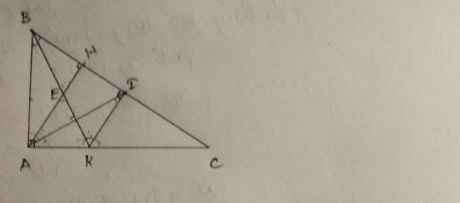
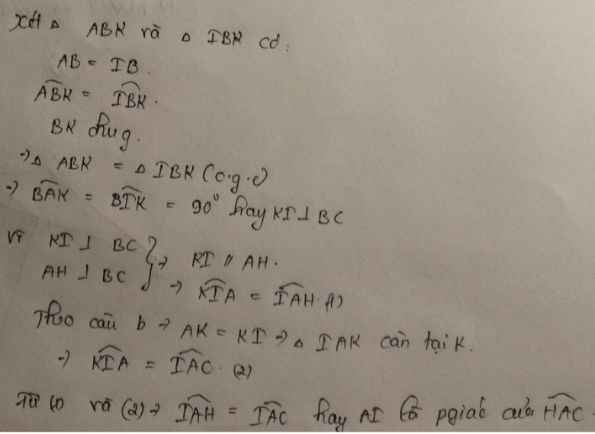
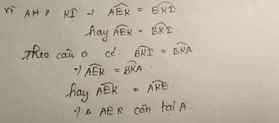
a, b ,c lần lượt từ trên xuống.