Giải giúp mình câu 1 với câu 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
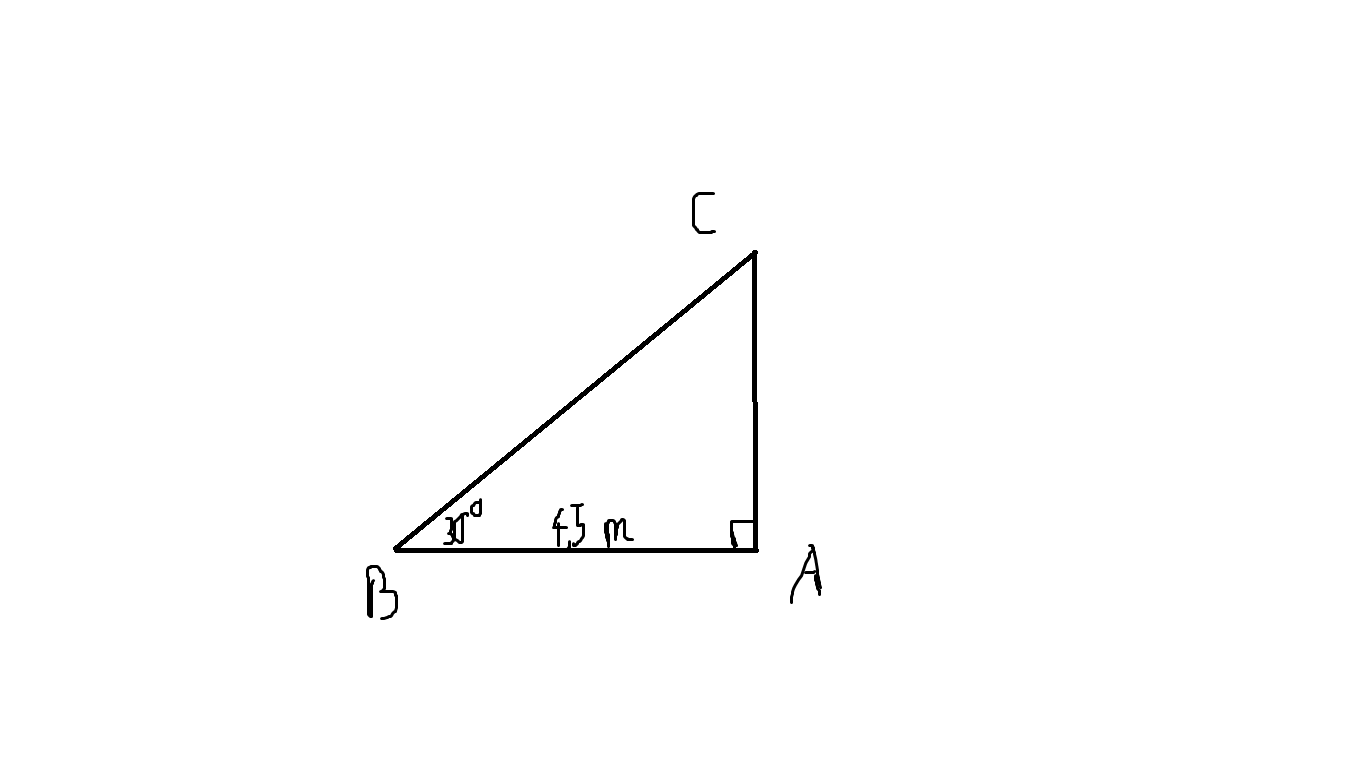
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)


Làm thế này nhé
(2x-6)y+x-3=18
(2x-6)y+x-18-3=0
(2x-6)y+x-21=0
sau đó bạn rút gọn nhé, ta làm như sau
2(x-3)=0
=> 2x= 2 x 3
=> x=3 nhé
giúp mình llàm câu b với nhé đã k cho bạn rồi nha
b, y = \(\frac{23}{x+7}\)



Câu 4:
Thay x=2 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)

V R2 R1 R3 A B
Tóm tắt:
\(R_2=4\Omega\\ R_3=15\Omega\\ I_3=0,2A\\ U_2=1,2V\\ R_1=?\)
Giải:
Cấu tạo \(\left(R_1ntR_2\right)\)//R3
\(I_2=\dfrac{U_2}{R_2}=\dfrac{1,2}{4}=0,3\left(A\right)\)
\(U_3=R_3\cdot I_3=13\cdot0,2=2,6\left(V\right)\)
\(U_{12}=U_3=2,6\Rightarrow U_1=U_3-U_2=2,6-1,2=1,4\left(V\right)\)
\(I_1=I_2=0,3A\Rightarrow R_1=\dfrac{U_1}{I_1}=\dfrac{1,4}{0,2}=7\left(\Omega\right)\)






