hàm số y= -x^2+mx-2/x+1 giảm trên từng khoảng xác định khi
giải chi tiết
cần gâp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ: x<>m
=>TXĐ: D=R\{m}
\(y=\dfrac{mx-2m-3}{x-m}\)
=>\(y'=\dfrac{\left(mx-2m-3\right)'\cdot\left(x-m\right)-\left(mx-2m-3\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-2m-3\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+2m+3}{\left(x-m\right)^2}=\dfrac{-m^2+2m+3}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\in TXĐ\)
=>\(\dfrac{-m^2+2m+3}{\left(x-m\right)^2}>0\)
=>\(-m^2+2m+3>0\)
=>\(m^2-2m-3< 0\)
=>(m-3)(m+1)<0
TH1: \(\left\{{}\begin{matrix}m-3>0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m< -1\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}m-3< 0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m< 3\end{matrix}\right.\)
=>-1<m<3
b: TXĐ: D=R\{m}
\(y=\dfrac{mx-4}{x-m}\)
=>\(y'=\dfrac{\left(mx-4\right)'\left(x-m\right)-\left(mx-4\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-4\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+4}{\left(x-m\right)^2}=\dfrac{-m^2+4}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(\dfrac{-m^2+4}{\left(x-m\right)^2}>0\)
=>\(-m^2+4>0\)
=>\(-m^2>-4\)
=>\(m^2< 4\)
=>-2<m<2

a: ĐKXĐ: x<>-m
=>TXĐ: D=R\{-m}
\(y=\dfrac{mx-2m+15}{x+m}\)
=>\(y'=\dfrac{\left(mx-2m+15\right)'\left(x+m\right)-\left(mx-2m+15\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{m\left(x+m\right)-mx+2m-15}{\left(x+m\right)^2}\)
\(=\dfrac{m^2+2m-15}{\left(x+m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định là \(y'>0\forall x\in TXĐ\)
=>\(\dfrac{m^2+2m-15}{\left(x+m\right)^2}>0\)
=>\(m^2+2m-15>0\)
=>(m+5)(m-3)>0
TH1: \(\left\{{}\begin{matrix}m+5>0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m>-5\end{matrix}\right.\)
=>m>3
TH2: \(\left\{{}\begin{matrix}m+5< 0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -5\\m< 3\end{matrix}\right.\)
=>m<-5
b: TXĐ: D=R\{-m}
\(y=\dfrac{mx+4m}{x+m}\)
=>\(y'=\dfrac{\left(mx+4m\right)'\left(x+m\right)-\left(mx+4m\right)\left(x+m\right)'}{\left(x+m\right)^2}\)
\(=\dfrac{m\left(x+m\right)-mx-4m}{\left(x+m\right)^2}\)
\(=\dfrac{mx+m^2-mx-4m}{\left(x+m\right)^2}=\dfrac{m^2-4m}{\left(x+m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m^2-4m}{\left(x+m\right)^2}>0\)
=>\(m^2-4m>0\)
=>\(m\left(m-4\right)>0\)
TH1: \(\left\{{}\begin{matrix}m>0\\m-4>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>0\\m>4\end{matrix}\right.\)
=>m>4
TH2: \(\left\{{}\begin{matrix}m< 0\\m-4< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< 0\\m< 4\end{matrix}\right.\)
=>m<0

Đáp án C
Ta có y ' = 2 − m x + 2 2 . Hàm số đồng biến trên từng khoảng xác định y ' > 0 , ∀ x ∈ D ⇔ 2 − m > 0 ⇔ m < 2 .

\(y'=\dfrac{-2m-1}{\left(x-2\right)^2}\)
\(y'< 0\) với mọi x thuộc TXĐ \(\Leftrightarrow-2m-1< 0\Leftrightarrow m>-\dfrac{1}{2}\)

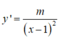
Để hàm số tăng trên từng khoảng xác định thì y’ > 0 <=> m > 0.
Chọn A

Đáp án A
Ta có y ' = − m + 1 x − 1 2
hàm số đồng biến trên từng khoảng xác định của nó ⇔ y ' > 0 ⇔ − m − 1 > 0 ⇔ m < − 1

Đáp án D
Ta có y ' = 1 − m x + 1 2
Để hàm số đồng biến trên từng khoảng xác định
⇔
y
'
>
0
,
∀
x
∈
D
=
ℝ
\
±
1
⇒
1
−
m
>
0
⇔
m
<
1

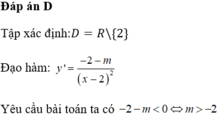
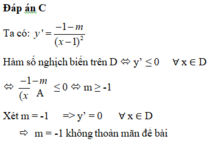
\(y=\dfrac{-x^2+mx-2}{x+1}\)
\(y'=\dfrac{\left(-2x+m\right)\left(x+1\right)-\left(-x^2+mx-2\right)}{\left(x+1\right)^2}=\dfrac{-x^2-2x+m+2}{\left(x+1\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi:
\(-x^2-2x+m+2\le0;\forall m\)
\(\Leftrightarrow\Delta'=1+\left(m+2\right)\le0\)
\(\Rightarrow m\le-3\)