Cho( P ): y=x2 và đường thẳng ( D ): y=2x + m - 3. Biện luận theo m số giao điểm của ( D ) và ( P)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
13 tháng 5 2021
Vì đường thẳng (d) cắt Oy tại điểm có tung độ bằng 8
Nên m+3=8⇔ m=5
Theo pt hoành độ giao điểm của (d) và (P)
Ta có:x2=2x+8x2=2x+8
⇔x2−2x−8=0x2−2x−8=0
Δ′=(−1)2−(−8)=9Δ′=(−1)2−(−8)=9
√Δ′=√9=3>0Δ′=9=3>0
Vậy pt có 2 nghiệm pb
x1=1+31=41+31=4
x2=1−31=−21−31=−2
Với x =4 thì y=x2=42=16
Với x =-2 thì y=x2=(-2)2=4
PT
0
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2022
a. Bạn tự giải
b. Pt hoành độ giao điểm: \(x^2=mx-m+1\Leftrightarrow x^2-mx+m-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=m-1\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x_1=1\\x_2=m-1\end{matrix}\right.\) \(\Rightarrow1=9\left(m-1\right)\Rightarrow m=\dfrac{10}{9}\)
TH2: \(\left\{{}\begin{matrix}x_1=m-1\\x_2=1\end{matrix}\right.\) \(\Rightarrow m-1=9.1\Rightarrow m=10\)
DD
Đoàn Đức Hà
Giáo viên
23 tháng 4 2022
Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là:
\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1)
Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo hệ thức Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)
Ta có hệ:
\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)
Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).
Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)
23 tháng 4 2022
Phương trình hoành độ giao điểm của (d)(d) và (P)(P) là:
x2=2mx+3⇔x2−2mx−3=0x2=2mx+3⇔x2−2mx−3=0 (1)
Phương trình (1) có hệ số a.c=1.(−3)=−3<0a.c=1.(−3)=−3<0 nên (1) luôn có hai nghiệm phân biệt x1,x2x1,x2.
Theo hệ thức Viete ta có:
{x1+x2=2mx1x2=−3{x1+x2=2mx1x2=−3
Ta có: |x1|+3|x2|=6|x1|+3|x2|=6
Ta có hệ:
{x1x2=−3|x1|+3|x2|=6⇔⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x1=−3x2∣∣∣3x2∣∣∣+3|x2|=6⇔⎧⎪⎨⎪⎩x1=−3x2x22−2|x2|+1=0{x1x2=−3|x1|+3|x2|=6⇔{x1=−3x2|3x2|+3|x2|=6⇔{x1=−3x2x22−2|x2|+1=0
⇔[x2=−1,x1=3x2=1,x1=−3⇔[x2=−1,x1=3x2=1,x1=−3
Với x1=3,x2=−1⇒x1+x2=2⇒m=1x1=3,x2=−1⇒x1+x2=2⇒m=1.
Với x1=−3,x2=1⇒x1+x2=−2⇒m=−1x1=−3,x2=1⇒x1+x2=−2⇒m=−1
CM
25 tháng 9 2017
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
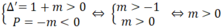
Khi đó 2 nghiệm của phương trình là:
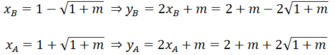
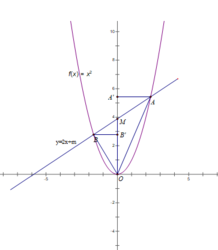
Kẻ BB' ⊥ OM ; AA' ⊥ OM
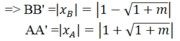
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
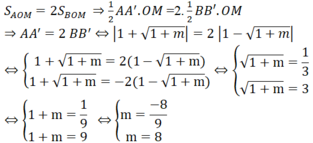
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
T
5 tháng 5 2023
a, Hoành độ giao điểm của d và P là:
x2 = 2mx -m +1 <=> x2 -2mx +m-1
đenta = 4m2-4.(m-1) = 4m2-4m+4 = (2m)2-2.2m +1 +3=(2m-1)2+3
=> đenta >= 3
Vậy không có giá trị m để P tiếp xúc với d
b,Áp dụng định lí Vi-ét:
\(\left\{{}\begin{matrix}x1+x2=2m\\x1.x2=m-1\end{matrix}\right.\)
Ta có: x12.x2 + mx2=x2
<=> x12.x2+mx2-x2=0 <=> x12.x2 + x2(m-1)=0
<=> x12.x2+x2(x1.x2)=0 <=>x12.x2+x22.x1=0
<=>x1.x2.(x1+x2)=0 <=> (m-1).2m=0
<=> \(\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Vậy m \(\in\) \(\left\{1;0\right\}\)
Hoành độ Giao điểm chính là nghiệm của D=P vậy ta xem nó có bao nhiêu nghiệm
x^2=2x+m-3
(x-1)^2=m-4
Nếu m=4 => có một nghiệm x=1 có 1 giao điểm
nếu m<4 => không tồn tại x => không có giao điểm
m>4 => \(\orbr{\begin{cases}x=1-\sqrt{m-4}\\x=1+\sqrt{m-4}\end{cases}}\) => có 2 điểm
Thank you