Cho biểu thức:456-m+56 A tính giá trị của biểu thức với m=74;m=9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)
\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)
Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)
Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)
a) \(P=1957\)
b) \(S=19.\)

a) Với m = 0, giá trị biểu thức 12 : (3 – m) là:
12 : (3 – 0) = 12 : 3 = 4
Với m = 1, giá trị biểu thức 12 : (3 – m) là:
12 : (3 – 1 ) = 12 : 2 = 6
Với m = 2, giá trị biểu thức 12 : (3 – m) là:
12 : (3 – 2) = 12 : 1 = 12
b) Vì 4 < 6 < 12 nên trong ba giá trị tìm được ở câu a, với m = 2 thì biểu thức 12 : (3 – m) có giá trị lớn nhất.

a) P=X -342
= 1000 - 342
= 658
P = 0
=> X -342 = 0
=> X = 342

Đáp án A
M = 5 6 : 5 2 2 + 7 15 M = 5 6 : 25 4 + 7 15 M = 5 6 . 4 25 + 7 15 M = 1 . 2 3 . 5 + 7 15 M = 2 15 + 7 15 M = 9 15 = 3 5
Khi đó a = 3,b = 5 nên a + b = 8

Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

a, a x 6 = 3 x 6 = 18
b, a + b = 4 + 2 = 6
c, b + a = 2 + 4 = 6
d, a - b = 8 - 5 = 3
e, m x n = 5 x 9 = 45

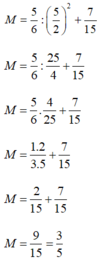
`@` Với `m=74` có: `456-74+56=382+56=438`
`@` Với `m=9` có: `456-9+56=447+56=503`
\(\odot\) với \(m=74\)
Thay \(m=74\) vào biểu thức trên ta được :
\(=456-74+56\\ =438\)
Vậy với \(m=74\) thì giá trị biểu thức \(=438\)
\(\odot\) với \(m=9\)
Thay \(m=9\) vào biểu thức trên ta được :
\(=456-9+56\\ =503\)
Vậy với \(m=9\) thì giá trị biểu thức \(=503\)