khi nào x mũ 2022=x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
8 tháng 10 2023
\(\left(x-5\right)^{2022}=\left(x-5\right)^{2024}\\ \Rightarrow\left(x-5\right)^{2022}-\left(x-5\right)^{2024}=0\\ \Rightarrow\left(x-5\right)^{2022}\left[1-\left(x-5\right)^2\right]=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-5\right)^{2022}=0\\1-\left(x-5\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\\left(x-5\right)^2=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\\left(x-5\right)^2=\left(\pm1\right)^2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=6\\x=4\end{matrix}\right.\)
8 tháng 10 2023
`#3107.101107`
\(\left(x-5\right)^{2022}=\left(x-5\right)^{2024}\)
\(\Rightarrow\left(x-5\right)^{2022}-\left(x-5\right)^{2024}=0\\ \Rightarrow\left(x-5\right)^{2022}\cdot\left[1-\left(x-5\right)^2\right]=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-5\right)^{2022}=0\\1-\left(x-5\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\\left(x-5\right)^2=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\\left(x-5\right)^2=\left(\pm1\right)^2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x-5=1\\x-5=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=6\\x=4\end{matrix}\right.\)
Vậy, \(x\in\left\{4;5;6\right\}.\)
6P
1
Z
2
S
29 tháng 3 2023
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{x}=\dfrac{x+y+z}{y+z+x}=\dfrac{x+y+z}{x+y+z}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=x\end{matrix}\right.\)
Do đó \(\left\{{}\begin{matrix}x-y=0\\y-z=0\\z-x=0\end{matrix}\right.\)
Thay vào biểu thức \(P=\left(x-y\right)^{2022}+\left(y-z\right)^{2023}+\left(x-z-1\right)^{202}\),ta có:
\(P=0^{2022}+0^{2023}+\left(-1\right)^{202}\)
\(=0+0+1\)
\(=1\)
5 tháng 8 2023
Bài 9,
62x73+36x33=36x73+36x27=36(73+27)=36x100=3600.
197-\([\)6x(5-1)2+20220\(]\):5=197-\([\)6x16+1\(]\):5=197-97:5=197-97/5=888/5.
Bài 10,
21-4x=13
=>4x=21-13=8
=>x=8:4=2.
30:(x-3)+1=45:43=42=16
=>30:(x-3)=16-1=15
=>x-3=30:15=2
=>x=2+3=5.
(x-1)3+5x6=38
=>(x-1)3+30=38
=>(x-1)3=38-30=8=23
=>x-1=2
=>x=3.
HD
2
4 tháng 9 2020
\(\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}=0\)
Vì \(\hept{\begin{cases}\left(x+1\right)^{2020}\ge0\forall x\\\left(2-3y\right)^{2022}\ge0\forall y\end{cases}}\Rightarrow\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}\ge0\forall x,y\)
Dấu " = " xảy ra khi và chỉ khi \(\hept{\begin{cases}\left(x+1\right)^{2020}=0\\\left(2-3y\right)^{2022}=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\3y=2\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\y=\frac{2}{3}\end{cases}}\)
4 tháng 9 2020
( x + 1 )2020 + ( 2 - 3y )2022 = 0
Ta có \(\hept{\begin{cases}\left(x+1\right)^{2020}\ge0\forall x\\\left(2-3y\right)^{2022}\ge0\forall y\end{cases}}\Rightarrow\left(x+1\right)^{2020}+\left(2-3y\right)^{2022}\ge0\forall x,y\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x+1=0\\2-3y=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\y=\frac{2}{3}\end{cases}}\)
Vậy x = -1 ; y = 2/3
30 tháng 9 2023
\(S=1+3^2+3^4+...+3^{2022}\)
\(3^2S=9S=3^2+3^4+3^6+...+3^{2024}\)
\(S=\dfrac{9S-S}{8}=\left(3^{2024}-1\right):8\)
d, không đáp án nào đúng
AH
Akai Haruma
Giáo viên
30 tháng 9 2023
Lời giải:
$S=1+3^2+3^4+....+3^{2022}$
$9S=3^2S=3^2+3^4+3^6+...+3^{2024}$
$\Rightarrow 9S-S=3^{2024}-1$
$\Rightarrow S=\frac{3^{2024}-1}{8}$
Đáp án D.
12 tháng 8 2023
a)\(27.65+27.35+300=27.\left(65+35\right)+300\)
\(=27.100+300=2700+300=3000\)
b)\(3838:\left[\left(190-6.5^2\right):4+3\right]\)
\(=3838:\left[\left(190-6.25\right):4+3\right]\)
\(=3838:\left[\left(190-150\right):4+3\right]\)
\(=3838:\left[40:4+3\right]=3838:\left[10+3\right]\)
\(=3838:13=\dfrac{3838}{13}\)
c)\(2022-x=2021\)
\(x=2022-2021=1\)
d)\(26+14:\left(x-5\right)=33\)
\(14:\left(x-5\right)=33-26=7\)
\(x-5=14+7=2\)
\(x=2+5=7\)
e)đề hỏi làm j thế bạn
TH
1
17 tháng 3 2023
\(=\dfrac{-2}{3}\cdot\dfrac{12}{19}-\dfrac{2}{3}\cdot\dfrac{7}{19}+1\)
=-2/3(12/19+7/19)+1
=1-2/3
=1/3
27 tháng 7 2021
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
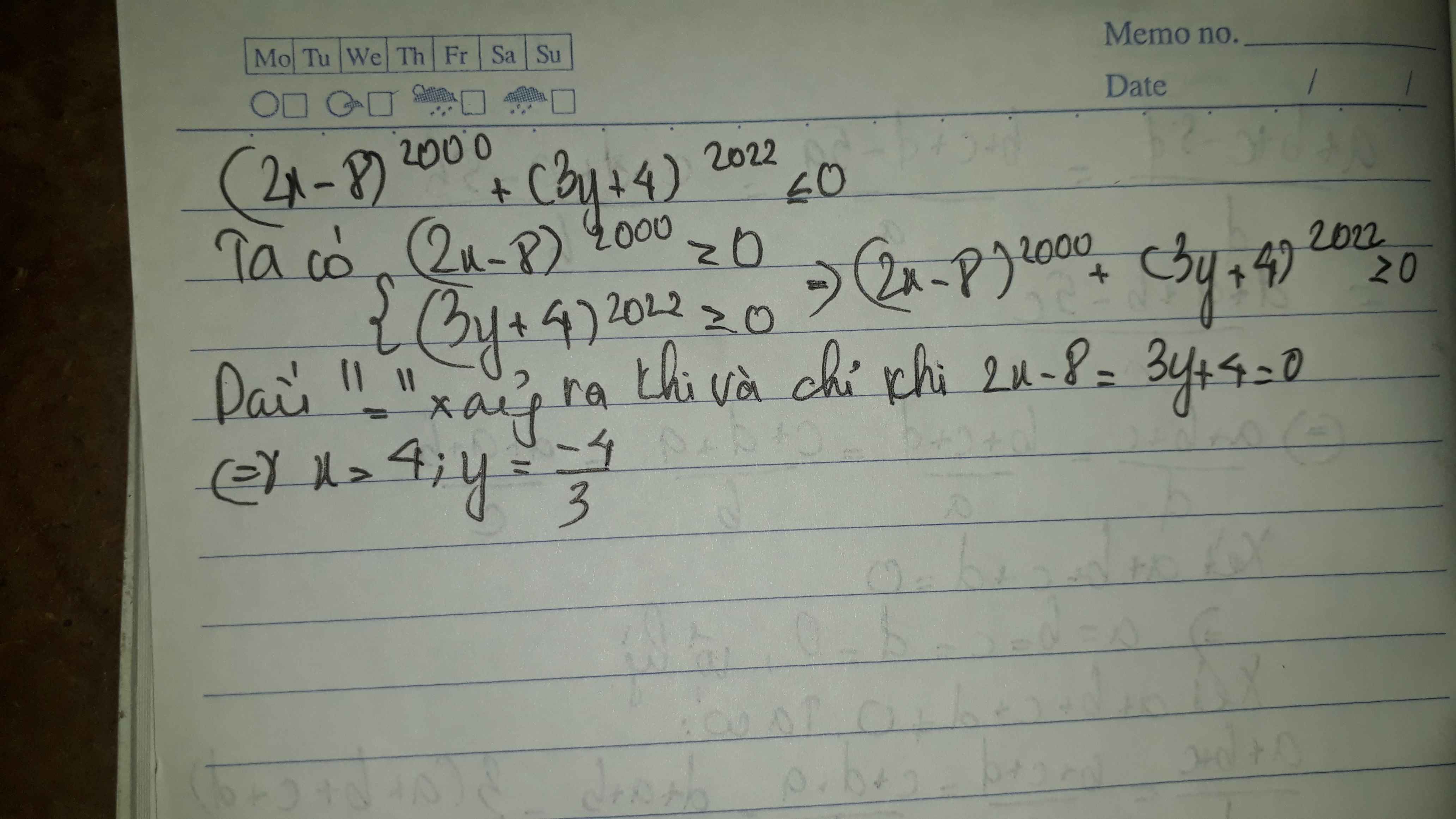
x2022 = x
⇔ x2022 - x = 0
⇔ x.(x2021 - 1) = 0
⇔ x=0; hoặc x2021 = 1
⇔ x = 0; x = 1
Lời giảiL
$x^{2022}=x$
$x^{2022}-x=0$
$x(x^{2021}-1)=0$
$\Rightarrow x=0$ hoặc $x^{2021}=1$
Hay $x=0$ hoặc $x=1$