E=a+a3+a5+...+a2n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
2
23 tháng 8 2021
\(P=a+a^2+a^3+...+a^{2n}=\left(a+a^2\right)+\left(a^3+a^4\right)+...+\left(a^{2n-1}+a^{2n}\right)=a\left(a+1\right)+a^3\left(a+1\right)+...+a^{2n-1}\left(a+1\right)=\left(a+1\right)\left(a+a^3+...+a^{2n-1}\right)⋮a+1\)
23 tháng 8 2021
Ta có: \(P=a+a^2+a^3+...+a^{2n}\)
\(=a\left(1+a\right)+a^3\left(1+a\right)+...+a^{2n-1}\left(1+a\right)\)
\(=\left(a+1\right)\left(a^{2n-1}+...+a^3+a\right)⋮a+1\)
MC
1
TN
7 tháng 9 2017
Ko mất tính tổng quát giả sử \(a_1=\text{max}\left\{a_2;a_3;a_4;a_5\right\}\).
Áp dụng BĐT AM-GM ta có:
\(a_1a_2+a_2a_3+a_3a_4+a_4a_5\le a_1\left(a_2+a_3+a_4+a_5\right)\)
\(\le\frac{\left(a_1+a_2+a_3+a_4+a_5\right)^2}{4}=\frac{1}{4}\)
Xảy ra khi có 2 số bằng \(\frac{1}{2}\) và 3 số còn lại bằng 0
MC
0
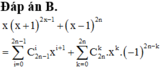
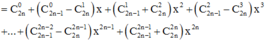
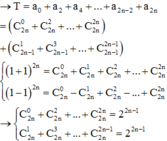
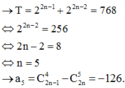
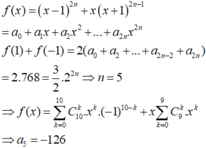
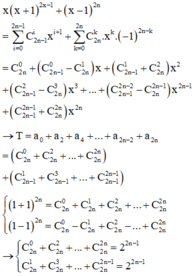
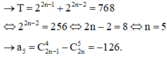
Ta có :
E=a+a3+a5+...+a2n+1
=> a2.E=a3+a5+a7+...+a2n+3
=> a2.E-E=(a3+a5+a7+...+a2n+3)-(a+a3+a5+...+a2n+1)
=> (a2-1).E=a2n+3-1
=> E=\(\dfrac{a^{2n+3}-1}{a^2-1}\)