Tính diện tích hình tam giác bết góc B=30 độ và AB=12cm,BC=15cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


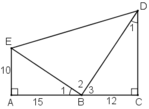
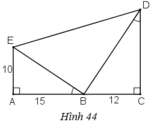
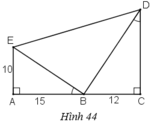
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
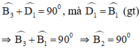
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
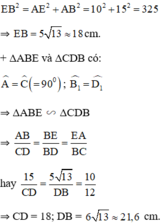
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
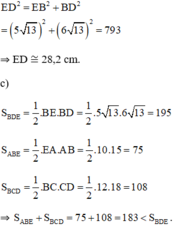

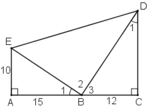
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
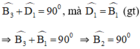
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
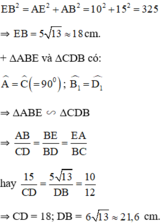
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
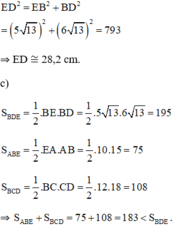

a) Từ chu vi tính được cạnh tam giác đều là 30 : 3 = 10 ( cm)
Kẻ đường cao AH xuống BC, H thuộc BC
Dùng Pytago tìm được AH = \(5\sqrt{3}\)
Diện tích tam giác ABC là AH . BC = \(50\sqrt{3}\)
Vậy ...

A M N H C B
Cho tam giác ABC có MN =15 cm NK =12 cm
Xét: Tam giác AHB (HBN) = 90 độ HM = đc
Xét tam giác AHC (AHC = 90 độ) có HN là đường cao
=> AH =An = AC (2)
Kết luận sơ sơ: Từ (1) (2) AM AB =AN=AC
...................... còn lại chịu -.-
~Study well~ :)

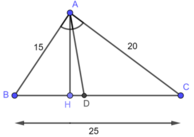
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

P/s bạn kia làm cái gì mà mình không hiểu
a) có AB = 15cm ( bài cho)
Xét tam giác AHC có góc AHC = 90 độ( AH vuông góc với BC)
theo định lý py-ta-go có
AB^2= AH^2+BH^2
=> BH^2 = AB^2 - AH^2
=> BH^2= 15^2- 12^2= 81
=> BH= 9
có BH+ HC=BC => BC= 9+16= 25
Vậy ta có AB= 15cm; BC= 25cm
câu sau tương tự bạn đó ( câu đầu làm mình không thấy tính AB với BC đâu hết )
a)Ta có: \(AC^2=AH^2+HC^2\)(định lý pytago)
\(\Rightarrow AC^2=12^2+16^2=144+256=400\)
\(\Rightarrow AC=20cm\)
b)Ta có:\(\widehat{HAC}\)\(+\)\(\widehat{AHC}\)\(+\)\(\widehat{ACH}\)\(=180^o\)(tổng 3 góc trong 1 tam giác)
\(\Rightarrow\widehat{ACH}\)\(=180^o\)\(-\widehat{HAC}\)\(-\widehat{AHC}\)\(=180^o\)\(-37^o-90^o=53^o\)
ta có:\(\widehat{ABC}\)\(=\widehat{HAC}\)\(+\widehat{ACH}\)(tính chất góc ngoài của tam giác)
Hay:\(\widehat{ABC}\)\(=37^o+53^o=90^o\)