Giải phương trình:
8x2+ 10x +3 =1/ 4x2 + 7x+3
Giúp dùm cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, 3x2 - 8x2 - 2x+3=0
2x(3-8) - 2x+3=0
2x5 - 2x+3=0
2x5 - 2x=0-3=
2x5 - 2x=-3
2x(5-x)=-3
5-x=-3/2
5-x=1,5
x=5-1,5
x=3,5

a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)

`d,(10x+3)/12=1+(6+8x)/9`
`<=>(10x+3)/12=(8x+15)/9`
`<=>30x+9=32x+60`
`<=>2x=-51`
`<=>x=-51/2`

Điều kiện của phương trình là 4 x 2 + 7 x - 2 ≥ 0 và x ≠ -2. Ta có
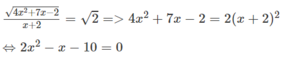
Phương trình cuối có hai nghiệm là x 1 = 5/2, x 2 = -2
Chỉ có giá trị x 1 = 5/2, x 2 = -2
Chỉ có giá trị x 1 = 5/2 thỏa mãn điều kiện và nghiệm đúng phương trình đã cho.
Đáp số: x = 5/2

a: (x^2+x)^2+4x^2+4x-12
=(x^2+x)^2+4(x^2+x)-12
=(x^2+x+6)(x^2+x-2)
=(x^2+x+6)(x+2)(x-1)
b: =(x^2+8x)^2+22(x^2+8x)+105+15
=(x^2+8x)^2+22(x^2+8x)+120
=(x^2+8x+10)(x^2+8x+12)
=(x^2+8x+10)(x+2)(x+6)
c: =8x^2+12x-2x-3
=(2x+3)(4x-1)

a: =(x^2+x)^2+4(x^2+x)-12
=(x^2+x+6)(x^2+x-2)
=(x^2+x+6)(x+2)(x-1)
b: =(x^2+8x)^2+22(x^2+8x)+120
=(x^2+8x+12)(x^2+8x+10)
=(x+2)(x+6)(x^2+8x+10)
c: =8x^2+12x-2x-3
=(2x+3)(4x-1)
Ta có:\(8x^2+10x+3=\left(8x^2+6x\right)+\left(4x+3\right)\)
\(=2x\left(4x+3\right)+\left(4x+3\right)\)
\(=\left(2x+1\right)\left(4x+3\right)\)
\(4x^2+7x+3=\left(4x^2+4x\right)+\left(3x+3\right)\)
\(=4x\left(x+1\right)+3\left(x+1\right)\)
\(=\left(x+1\right)\left(4x+3\right)\)
\(ĐKXĐ:x\ne-1,x\ne\frac{-3}{4}\)
\(8x^2+10x+3=\frac{1}{4x^2+7x+3}\)
<=>\(\left(8x^2+10x+3\right)\left(4x^2+7x+3\right)=1\)
<=>\(\left(2x+1\right)\left(4x+3\right)\left(x+1\right)\left(4x+3\right)=1\)
<=>\(\left(2x+1\right)\left(4x+3\right)^2\left(x+1\right)=1\)
<=>\(\left(4x+2\right)\left(4x+3\right)^2\left(4x+4\right)=8\)
(Nhân cả 2 vế với 8)
<=>\(\left[\left(4x+2\right)\left(4x+4\right)\right]\left(4x+3\right)^2=8\)
<=>\(\left(16x^2+24x+8\right)\left(16x^2+24x+9\right)=8\)
Đặt \(16x^2+24x+8.5=y\)
\(ĐK:y>-0.5\)
(Vì \(16x^2+24x+8.5=\left(4x+3\right)^2-0.5>-0.5\)với mọi x thỏa mãn ĐKXĐ)
Phương trình trở thành:
(y-0.5)(y+0.5)=8
<=>\(y^2-0.25=8\)
<=>\(y^2=8.25\)
<=>\(\orbr{\begin{cases}y=\frac{\sqrt{33}}{2}\left(\text{thỏa mãn}\right)\\y=\frac{-\sqrt{33}}{2}\left(\text{loại}\right)\end{cases}}\)
Với \(y=\frac{\sqrt{33}}{2}\)
Ta có:\(16x^2+24x+8.5=\frac{\sqrt{33}}{2}\)
<=>\(32x^2+48x+17-\sqrt{33}=0\)
<=>\(\left(x\sqrt{33}+3\sqrt{2}\right)^2=\sqrt{33}+1\)
<=>\(\orbr{\begin{cases}x\sqrt{33}+3\sqrt{2}=\sqrt{\sqrt{33}+1}\\x\sqrt{33}+3\sqrt{2}=-\sqrt{\sqrt{33+1}}\end{cases}}\)
<=>\(\orbr{\begin{cases}x=\frac{\sqrt{\sqrt{33}+1}-3\sqrt{2}}{\sqrt{33}}\\x=\frac{-\sqrt{\sqrt{33}+1}-3\sqrt{2}}{\sqrt{33}}\end{cases}}\)
<=>\(\orbr{\begin{cases}x=\frac{\sqrt{33\sqrt{33}+33}-3\sqrt{66}}{33}\left(\text{thỏa mãn ĐKXĐ}\right)\\x=\frac{-\sqrt{33\sqrt{33}+33}-3\sqrt{66}}{33}\left(\text{thỏa mãn ĐKXĐ}\right)\end{cases}}\)
(Kết luận: Vậy tập nghiệm của phương trình đã cho là...)