(x+1) (x mũ 2-x+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
2\(x\) = 4
2\(^x\) = 22
\(x=2\)
Vậy \(x=2\)
Bài 2:
2\(^x\) = 8
2\(^x\) = 23
\(x=3\)
Vậy \(x=3\)

Câu a :
\(\left(2x+1\right)^2-4x\left(x-5\right)\)
\(=4x^2+4x+1-4x^2+20\)
\(=4x+19\)
Câu b :
\(\left(x+3\right)^2-\left(x+1\right)\left(x-1\right)\)
\(=x^2+6x+9-x^2-1\)
\(=6x-8\)
Câu c :
\(\left(x-5\right)^2-\left(x+2\right)^2\)
\(=\left(x-5-x-2\right)\left(x-5+x+2\right)\)
\(=-7\left(2x-3\right)\)

a) \(\left(x+3\right)^2-\left(x-4\right)\left(x+8\right)=1\)
\(\Leftrightarrow\left(x^2+6x+9\right)-\left(x^2+4x-32\right)-1=0\)
\(\Leftrightarrow2x=-40\)
\(\Rightarrow x=-20\)
b) \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-2\right)\left(x+2\right)=15\)
\(\Leftrightarrow x^3+27-x^3+4x=15\)
\(\Leftrightarrow4x=-12\)
\(\Rightarrow x=-3\)
c) \(\left(x-2\right)^2-\left(x+3\right)^2-4\left(x+1\right)=5\)
\(\Leftrightarrow\left(x^2-4x+4\right)-\left(x^2+6x+9\right)-\left(4x+4\right)=5\)
\(\Leftrightarrow-14x=14\)
\(\Rightarrow x=-1\)
d) \(\left(2x-3\right)\left(2x+3\right)-\left(x-1\right)^2-3x\left(x-5\right)=-44\)
\(\Leftrightarrow4x^2-9-\left(x^2-2x+1\right)-\left(3x^2-15x\right)=-44\)
\(\Leftrightarrow17x=-34\)
\(\Rightarrow x=-2\)
e) \(\left(x-2\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=49\)
\(\Leftrightarrow x^3-6x^2+12x-8-x^3+27+6x^2+12x+6=49\)
\(\Leftrightarrow24x=24\)
\(\Rightarrow x=1\)

a) 2( x - 1 )2 - 4( 3 + x )2 + 2x( x - 5 )
= 2( x2 - 2x + 1 ) - 4( 9 + 6x + x2 ) + 2x2 - 10x
= 2x2 - 4x + 2 - 36 - 24x - 4x2 + 2x2 - 10x
= ( 2x2 - 4x2 + 2x2 ) + ( -4x - 24x - 10x ) + ( 2 - 36 )
= -38x - 34
b) 2( 2x + 5 )2 - 3( 4x + 1 )( 1 - 4x )
= 2( 4x2 + 20x + 25 ) + 3( 4x + 1 )( 4x - 1 )
= 8x2 + 40x + 50 + 3( 16x2 - 1 )
= 8x2 + 40x + 50 + 48x2 - 3
= 56x2 + 40x + 47
c) ( x - 1 )3 - x( x - 3 )2 + 1
= x3 - 3x2 + 3x - 1 - x( x2 - 6x + 9 ) + 1
= x3 - 3x2 + 3x - x3 + 6x2 - 9x
= 3x2 - 6x
d) ( x + 2 )3 - x2( x + 6 )
= x3 + 6x2 + 12x + 8 - x3 - 6x2
= 12x + 8
e) ( x - 2 )( x + 2 ) - ( x + 1 )3 - 2x( x - 1 )2
= x2 - 4 - ( x3 + 3x2 + 3x + 1 ) - 2x( x2 - 2x + 1 )
= x2 - 4 - x3 - 3x2 - 3x - 1 - 2x3 + 4x2 - 2x
= -3x3 + 2x2 - 5x - 5
f) ( a + b - c )2 - ( b - c )2 - 2a( b - c )
= [ ( a + b ) - c ]2 - ( b2 - 2bc + c2 ) - 2ab + 2ac
= [ ( a + b )2 - 2( a + b )c + c2 ] - b2 + 2bc - c2 - 2ab + 2ac
= a2 + 2ab + b2 - 2ac - 2bc + c2 - b2 + 2bc - c2 - 2ab + 2ac
= a2
a) \(2\left(x-1\right)^2-4\left(3+x\right)^2+2x\left(x-5\right)\)
Dùng hẳng đẳng thức thứ nhất + hai :
= \(2\left(x^2-2\cdot x\cdot1+1^2\right)-4\left(3^2+2\cdot3\cdot x+x^2\right)+2x^2-10x\)
= \(2\left(x^2-2x+1\right)-4\left(9+6x+x^2\right)+2x^2-10x\)
= \(2x^2-4x+2-36-24x-4x^2+2x^2-10x\)
= \(-38x-34\)
b) 2(2x + 5)2 - 3(4x + 1)(1 - 4x)
Dùng đẳng thức thứ 1 + 3
= 2[(2x)2 + 2.2x.5 + 52 ] - (-3)[(4x)2 - 12 ]
= 2(4x2 + 20x + 25) - (-3).(16x2 - 1)
= 8x2 + 40x + 50 - (3 - 48x2)
= 8x2 + 40x + 50 - 3 + 48x2
= 56x2 + 40x + 47
c) (x - 1)3 - x(x - 3)2 + 1
Dùng đẳng thức 2 + 5:
= x3 - 3.x2.1 + 3.x.12 - 13 - x(x2 - 2.x.3 + 32) + 1
= x3 - 3x2 + 3x - 1 - x3 + 6x2 - 9x + 1
= (x3 - x3) + (-3x2 + 6x2) + (3x - 9x) + (-1 + 1)
= 3x2 - 6x
d) (x + 2)3 - x2(x + 6)
= x3 + 3.x2.2 + 3.x.22 + 23 - x3 - 6x2
= x3 + 6x2 + 12x + 8 - x3 - 6x2
= (x3 - x3) + (6x2 - 6x2) + 12x + 8 = 12x + 8
e) Dùng đẳng thức thứ 3,4 và 2
= x2 - 4 - (x3 + 3.x2.1 + 3.x.12 + 13) - 2x(x2 - 2.x.1 + 12)
= x2 - 4 - (x3 + 3x2 + 3x + 1) - 2x3 + 4x2 - 2x
= x2 - 4 - x3 - 3x2 - 3x - 1 - 2x3 + 4x2 - 2x
= (x2 - 3x2 + 4x2) + (-4 - 1) + (-x3 - 2x3) + (-3x - 2x)
= 2x2 - 5 - 3x3 - 5x
f) Đặt \(a+b-c=A\)
\(b-c=B\)
= \(A^2-B^2-2AB\)
= \(A^2-2AB+\left(-B\right)^2\)
\(=A^2-2AB+B^2\)
= (A - B)2
= (a + b - c - (b - c))2
= (a + b - c - b + c)2
= a2

a)<=>
A,=(x+y)(x-y)=x^2-y^2
x=(-1/2)^5:(1/2)^4=-1/2
x^2=1/4
y=8^2/(-2)^5=-2
y^2=4
A=1/4-4=-15/4

Bài 1
a) \(x=x^5\)
\(x^5-x=0\)
\(x\left(x^4-1\right)=0\)
\(x=0\) hoặc \(x^4-1=0\)
* \(x^4-1=0\)
\(x^4=1\)
\(x=1\)
Vậy x = 0; x = 1
b) \(x^4=x^2\)
\(x^4-x^2=0\)
\(x^2\left(x^2-1\right)=0\)
\(x^2=0\) hoặc \(x^2-1=0\)
*) \(x^2=0\)
\(x=0\)
*) \(x^2-1=0\)
\(x^2=1\)
\(x=1\)
Vậy \(x=0\); \(x=1\)
c) \(\left(x-1\right)^3=x-1\)
\(\left(x-1\right)^3-\left(x-1\right)=0\)
\(\left(x-1\right)\left[\left(x-1\right)^2-1\right]=0\)
\(x-1=0\) hoặc \(\left(x-1\right)^2-1=0\)
*) \(x-1=0\)
\(x=1\)
*) \(\left(x-1\right)^2-1=0\)
\(\left(x-1\right)^2=1\)
\(x-1=1\) hoặc \(x-1=-1\)
**) \(x-1=1\)
\(x=2\)
**) \(x-1=-1\)
\(x=0\)
Vậy \(x=0\); \(x=1\); \(x=2\)

`(2^x+1)^2 =25`
`=> (2^x+1)^2 = (+-5)^2`
\(\Rightarrow\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
\(\left(x+6\right)\left(5^x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\5^x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\5^x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=0\end{matrix}\right.\)
\(\left(x-3\right)^{2023}=x-3\)
\(\Rightarrow\left(x-3\right)^{2023}-\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left[\left(x-3\right)^{2022}-1\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x-3=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)

a) \(\left(2x-5\right)^2-\left(2x+3\right)\left(2x-3\right)=10\Leftrightarrow\left(4x^2-20x+25\right)-\left(4x^2-9\right)-10=0\)
\(\Leftrightarrow-20x+24=0\Leftrightarrow x=\frac{6}{5}\)
b) \(\left(4x-1\right)\left(x+2\right)-\left(2x+3\right)^2-5\left(x-1\right)=9\Leftrightarrow-10x-15=0\)
\(\Leftrightarrow x=\frac{-3}{2}\)
c) \(\left(x+1\right)^3-\left(x-1\right)^3-2=6\Leftrightarrow\left(x^3+3x^2+3x+1\right)-\left(x^3-3x^2+3x-1\right)-8=0\)
\(\Leftrightarrow6x^2-6=0\Leftrightarrow x=\pm1\)
d) \(\left(x+2\right)\left(x^2-2x+4\right)-\left(x+1\right)\left(x^2-x+1\right)-3\left(-x-2\right)=5\)
\(\Leftrightarrow\left(x^3+8\right)-\left(x^3+1\right)+3x+6=5\Leftrightarrow3x+8=0\Leftrightarrow x=\frac{-8}{3}\)
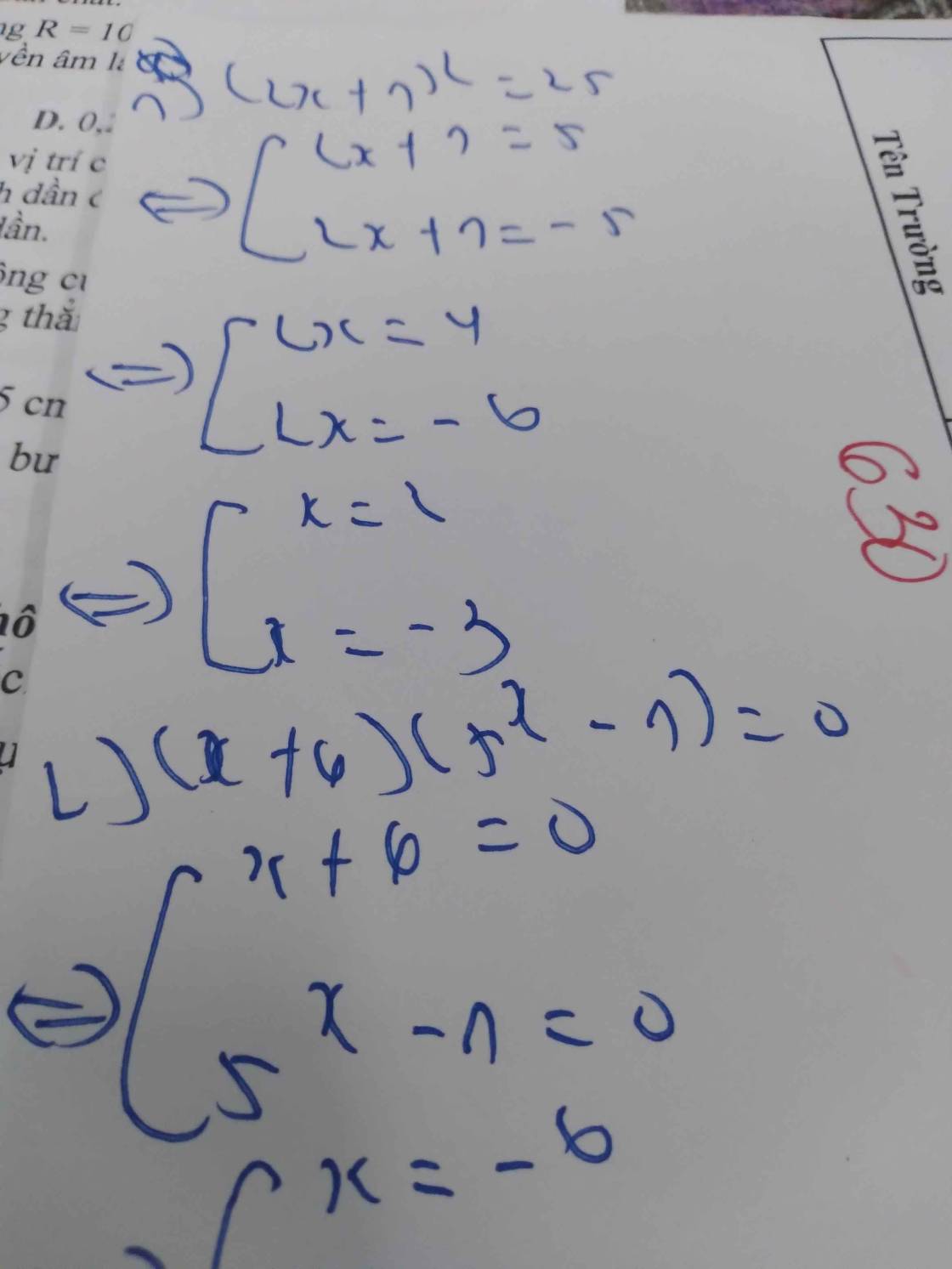


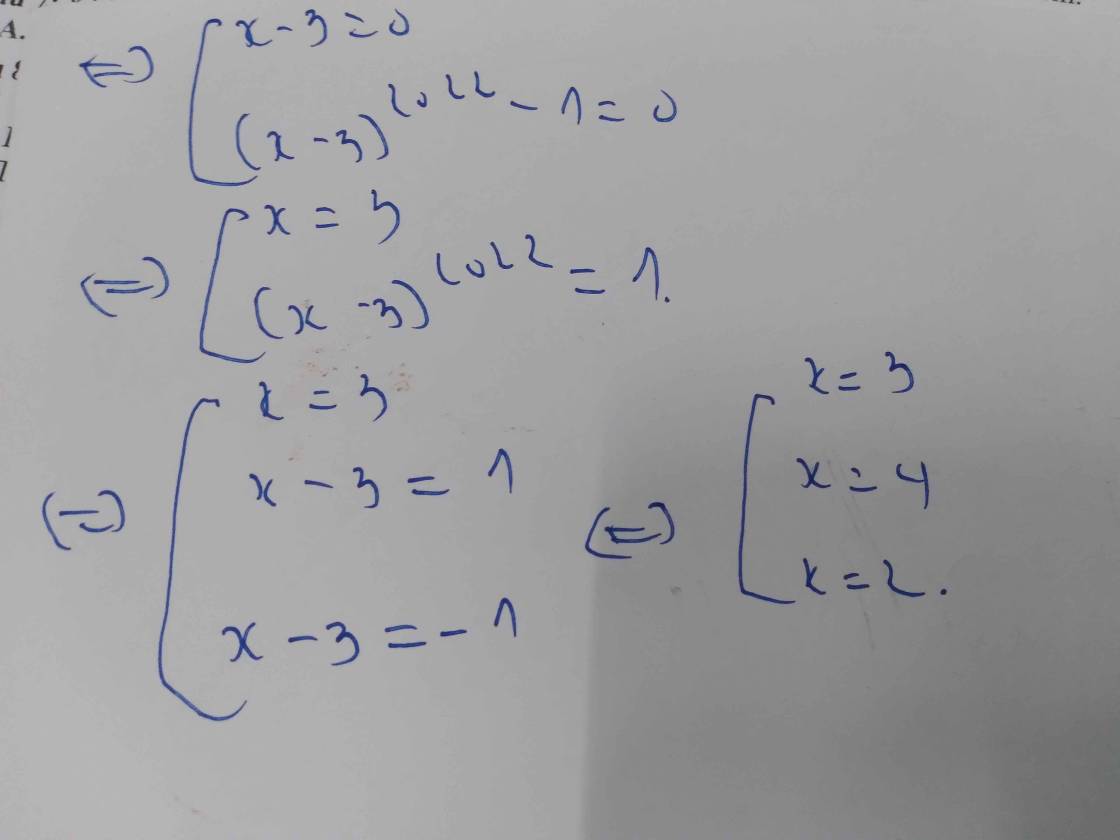
\(\left(x+1\right)\left(x^2-x+1\right)\\ =x^3+1^3\\ =x^3+1\)