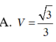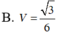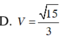Tính s ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 3 2019
Chọn đáp án A
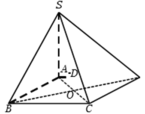
Đường chéo hình vuông AC = 2
Xét tam giác SAC, ta có
Chiều cao của khối chóp là SA = 3
Diện tích hình vuông ABCD là
Thể tích khối chóp S. ABCD là
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 5 2023
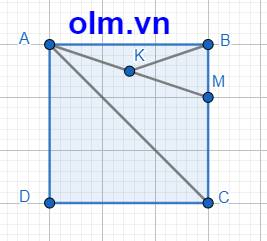
SABCD = 12 \(\times\)12 = 144 (cm2)
SABC = 12 \(\times\) 12 : 2 = 72 (cm2)
BM = 12 \(\times\) \(\dfrac{2}{3}\) = 8 (cm)
CM = 12 - 8 = 4 (cm)
SACM = 12 \(\times\)4 : 2 = 24 (cm2)
b, SABK = \(\dfrac{1}{2}\)SABM (vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáy BM và AK = \(\dfrac{1}{2}\)AM)
SABM = SABC - SAMC = 72 - 24 = 48 (cm2)
SABK = 48 : 2 = 24 (cm2)
Đáp số: a, SABCD = 144 cm2; SACM = 24 cm2
b, SABK = 24 cm2
CM
3 tháng 12 2019
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp chóp là giao điểm của trục của mặt đáy và mặt phẳng trung trực của 1 cạnh bên.
+) Áp dụng các kiến thức đã học tính bán kính mặt cầu. Từ đó áp dụng công thức tính diện tích mặt cầu bán kính R: S = 4 π R 2
Cách giải:
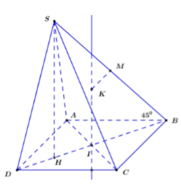
Qua I dựng đường thẳng d song song với SH, đường thẳng này chính là trục của hình chóp SABCD.
Dựng đường thẳng trung trực của cạnh SB,
cắt đường thẳng d tại K.
Khi đó K là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
14 tháng 7 2017
ra 6 bạn ạ nếu bài này có hình thì mk làm cho nhưng ko có hình thì kết quả thôi ha
19 tháng 3 2017
a) Kẻ BH vuông góc với AD.
SABCD=BH.AD=BH.2BM=S
=> BH.BM=\(\dfrac{S}{2}\)
Có AD song song với BM (ABCD là hbh)
SABMD=\(\dfrac{\left(AD+BM\right).BH}{2}=\dfrac{3BM.BH}{2}=\dfrac{3}{2}.\dfrac{S}{2}=\dfrac{3S}{4}\)
b) Nối A với M. T là trung điểm của AD. Nối B với T.
Ta có: TDMB là hbh (TD song song với BM; TD=BM=\(\dfrac{1}{2}BC\))
=> TF là đường TB của tam giác ADN => AF=FN (1)
MN là đường TB của tam giác BCF => FN=NC (2)
Từ (1)(2)=> AF=FN=NC
Ta có: SNMC=SFMN=SAFM
mà SABC =\(\dfrac{S}{2}\) và SABM=SACM => SAMC= \(\dfrac{S}{4}\)
=> SMNC = \(\dfrac{S}{4}:3=\dfrac{S}{12}\)
=> SABMN = SABC-SMNC = \(\dfrac{S}{2}-\dfrac{S}{12}=\dfrac{5S}{12}\)
DP
2 tháng 7 2017
A B C D E 30 cm H K
- \(S_{EBC}=S_{AED}=30cm^2\)
- \(S_{ABC}=\frac{1}{2}S_{ACD}\)Chiều cao bằng nhau , \(AB=\frac{1}{2}CD\)
2 tam giác này nếu lấy \(AC\)là đáy thì \(BK\)và \(DH\)là chiều cao tương ứng .
\(\Rightarrow BK=\frac{1}{2}DH\)
\(S_1=\frac{1}{2}S_3\)(chung đáy \(AE\))
\(BK=\frac{1}{2}DH\)
\(\Rightarrow S_1=\frac{1}{2}\cdot30=15\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=30+15=45\left(cm^2\right)\)
\(\Rightarrow S_{ACD}=45\cdot2=90\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=45+90=135\left(cm^2\right)\)
DP
2 tháng 7 2017
Xin lỗi mik nhìn nhầm 302 m2 thành 30m2
A B C D 302cm H K E
- \(S_{EBC}=S_{AED}=302\left(cm^2\right)\)
- \(S_{ABC}=\frac{1}{2}S_{ACD}\)(chiều cao bằng nhau) , \(AB=\frac{1}{2}CD\)
2 tam giác này nếu lấy \(AC\)là cạnh đáy thì \(BK\)và \(DH\)là chiều cao tương ứng
\(\Rightarrow BK=\frac{1}{2}DH\)
\(S_1=\frac{1}{2}S_3\)(chung đáy \(AE\))
\(\Rightarrow S_1=\frac{1}{2}\cdot302=151\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=302+151=453\left(cm^2\right)\)
\(\Rightarrow S_{ACD}=453\cdot2=906\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=453+906=1359\left(cm^2\right)\)
Đáp số "