a, (a+1).(b-1)=143
b, (a-2).(b+1)=95
Hãy tính a và b trong mỗi câu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,=157\times6-6\times143=6\times\left(157-143\right)=6\times14=84\\ b,=24\times5+189:9=120+21=141\\ 3,\)
Đợt thứ nhất nhận đc \(5376-254=5122\left(tạ\right)\)
Đợt thứ 2 nhận đc \(12044-5122=6922\left(tạ\right)\)
Đợt 2 nhập nhiều hơn \(6922-5122=1800\left(tạ\right)\)
Bạn ơi bạn viết lại bài 1 nó thành câu hoàn chỉnh được ko ? Please

Câu 2: Đó là các số tự nhiên 4 chữ số khác nhau. Vậy có 4536 số

Bài 1.
a) Cu có hóa trị ll.
O có hóa trị ll.
b) Ba có hóa trị ll.
NO3 có hóa trị l.
Bài 2.
a) \(BaO\Rightarrow137+16=153\left(đvC\right)\)
B) \(Al_2\left(SO_4\right)_3\Rightarrow2\cdot27+3\cdot32+16\cdot12=342\left(đvC\right)\)

Câu 3:
a, Ta có: \(n_{O_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
b, Ta có: 0,98 kg = 980 (g)
\(\Rightarrow n_{H_2SO_4}=\dfrac{980}{98}=10\left(mol\right)\)
c, Ta có: \(n_{O_2}=\dfrac{12.10^{22}}{6.10^{23}}=0,2\left(mol\right)\)
Câu 4:
Giả sử: \(\left\{{}\begin{matrix}n_{N_2}=x\left(mol\right)\\n_{O_2}=y\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{2}{1}\Leftrightarrow x-2y=0\left(1\right)\)
Mà: mA = 8,8 (g)
\(\Rightarrow28x+32y=8,8\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=0,2\left(mol\right)\\y=0,1\left(mol\right)\end{matrix}\right.\)
Bạn tham khảo nhé!

a) Đồ thị hàm số y = ax + b đi qua A(2; -2) ⇔ 2.a + b = -2 (1)
Đồ thị hàm số y = ax + b đi qua B(-1 ; 3) ⇔ a.(-1) + b = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
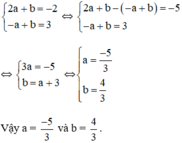
b) Đồ thị hàm số y = ax + b đi qua A(-4; -2) ⇔ a.(-4) + b = -2
Đồ thị hàm số y = ax + b đi qua B(2 ; 1) ⇔ a.2 + b = 1
Ta có hệ phương trình :
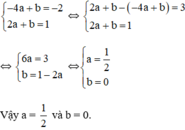
c) Đồ thị hàm số y = ax + b đi qua A(3 ; -1) ⇔ a.3 + b = -1
Đồ thị hàm số y = ax + b đi qua B(-3 ; 2) ⇔ a.(-3) + b = 2.
Ta có hệ phương trình :
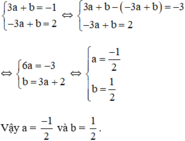
d) Đồ thị hàm số y = ax + b đi qua A(√3 ; 2) ⇔ a.√3 + b = 2 (*)
Đồ thị hàm số y = ax + b đi qua B(0; 2) ⇔ a.0 + b = 2 ⇔ b = 2.
Thay b = 2 vào (*) ta được a.√3 + 2 = 2 ⇔ a.√3 = 0 ⇔ a = 0.
Vậy a = 0 và b = 2.
Kiến thức áp dụng
+ Đồ thị hàm số y = f(x) đi qua điểm A(x0; y0) ⇔ y0 = f(x0).
+ Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

a)
$n_{Cl_2} : n_{O_2} = 1 : 2$
Suy ra :
$\%V_{Cl_2} = \dfrac{1}{1 + 2}.100\% = 33,33\%$
$\%V_{O_2} = \dfrac{2}{1 + 2}.100\% = 66,67\%$
b)
Coi $n_{Cl_2} = 1 (mol) \Rightarrow n_{O_2} = 2(mol)$
$\%m_{Cl_2} = \dfrac{1.71}{1.71 + 2.32}.100\% = 52,59\%$
$\%m_{O_2} = 100\% -52,59\% = 47,41\%$
c)
$M_A = \dfrac{71.1 + 32.2}{1 + 2} = 45(g/mol)$
$d_{A/B} = \dfrac{45}{28} = 1,607$

26 điểm tương ứng với 6 câu đúng và 4 câu sai.
Xét trường hợp câu 1-6 đúng, 7-10 sai: xác xuất để được 26 điểm là (0,25)^6.(0,75)^4
có 10C6 cách chọn trường hợp như vậy
=> xác xuất để được 26 điểm là: 10C6.(0,25)^6.(0,75)^4