Ace giải cho mik với :
Cho các số: 7 ; 13 ; 17 ; 26 ; 32 ; 35. Trong các số đó số các số là số nguyên tố và hợp số lần lượt là a và b. Tính 6a + 9b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NO
1
TM
10 tháng 12 2016
\(2n^2+n-7\) chia hết cho n-2
<=> \(2n^2-4n+5n-10+3\) chia hết cho n-2
<=>\(2n\left(n-2\right)+5\left(n-2\right)+3\) chia hết cho n-2
<=>\(\left(n-2\right)\left(2n+5\right)+3\) chia hết cho n-2
Mà \(\left(n-2\right)\left(2n+5\right)\) chia hết cho n-2 <=> 3 chia hết cho n-2
<=>\(n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
<=>\(n\in\left\{-1;1;3;5\right\}\)
Vậy ..............
8 tháng 4 2020
Gọi số tự nhiên đó là abb ( Vì theo đề bài, hàng chục và hàng đơn vị bằng nhau, nên kí hiệu giống nhau )
Ta có : a + b + b = 7
Vì 7 chia hết cho 7 => a + b + b chia hết cho 7 => abb chia hết cho 7
* Nếu cần tìm số thì ib mình :D *
H9
HT.Phong (9A5)
CTVHS
17 tháng 9 2023
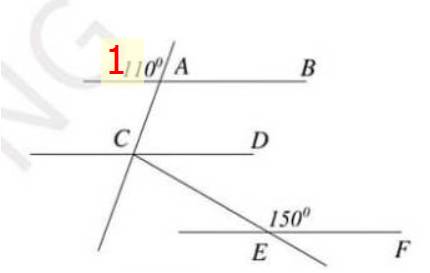
a) Ta có: AB//CD
\(\widehat{A_1}=\widehat{BAC}\)
\(\Rightarrow\widehat{BAC}=110^o\)
Mà: \(\widehat{BAC}+\widehat{ACD}=180^o\)
\(\Rightarrow\widehat{ACD}=180^o-110^o=70^o\)
Lại có: CD//EF
\(\Rightarrow\widehat{DCE}+\widehat{CEF}=180^o\)
\(\Rightarrow\widehat{DCE}=180^o-150^o=30^o\)
b) Mà: \(\widehat{ACE}=\widehat{ACD}+\widehat{DCE}\)
\(\Rightarrow\widehat{ACE}=30^o+70^o=100^o\)
23 tháng 5 2019
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
27 tháng 5 2019
Bổ đề: Cho tam giác ABC và tam giác DEF có ^BAC = ^EDF và \(\frac{AB}{DE}=\frac{AC}{DF}\). Khi đó ^ABC = ^DEF.
A B C D E F G H
Trên cạnh DE,EF của \(\Delta\)DEF lần lượt lấy các điểm G,H sao cho DG=AB, DH=AC.
Dễ thấy \(\Delta\)ABC = \(\Delta\)DGH (c.g.c) => ^ABC = ^DGH, Ta cũng có:
\(\frac{AB}{DE}=\frac{AC}{DF}\) hay \(\frac{DG}{DE}=\frac{DH}{DF}\). Suy ra \(\frac{S_{DHG}}{S_{DHE}}=\frac{S_{DGH}}{S_{DGF}}\)=> SDHE = SDGF
Do đó SEGH = SFHG => Khoảng cách từ E,F đến GH bằng nhau => GH // EF => ^DGH = ^DEF
Vậy nên ^ABC = ^DEF.
Quay trở lại bài toán:
A B C D E F P Q I J
Dựng Q đối xứng với F qua trung điểm P của AC.Gọi I là giao của AF và DE, DE cắt AC tại J.
Ta dễ thấy \(\Delta\)CPF = \(\Delta\)APQ (c.g.c) => FC=QA => QA = FB. Đồng thời ^PCF = ^PAQ.
Lại có biến đổi góc: ^DAQ = 3600 - ^DAB - ^BAC - ^PAQ = 3600 - 600 - ^BAC - ^PCF
= 3000 - ^BAC - ^ACB - 300 = 2700 - ^BAC - ^ACB = ^ABC + 900 = ^ABC + ^FBC + ^DBA = ^DBF
Xét \(\Delta\)DQA và \(\Delta\)DFB: DA=DF, ^DAQ = ^DBF, QA=FB => \(\Delta\)DQA = \(\Delta\)DFB (c.g.c)
=> DQ = DF và ^ADQ = ^BDF. Từ đây ^QDF = ^ADB = 600. Do đó \(\Delta\)QFD đều.
Mà P là trung điểm QF nên \(\Delta\)DPF nửa đều. Qua ĐL Pytagore ta dễ có \(\frac{PD}{PF}=\sqrt{3}\)
Để ý \(\Delta\)EPA nửa đều => \(\frac{PE}{PA}=\sqrt{3}\)=> \(\frac{PD}{PF}=\frac{PE}{PA}\).
Kết hợp với ^APF = ^EPD (=900 + ^APD) suy ra ^PAF = ^PED (Theo bổ đề) hay ^JAI = ^JEP
Mà ^AJI = ^EJP (Đối đỉnh) nên ^AIJ = ^EPJ = 900. Như vậy AF vuông góc DE (đpcm).
DL
11 tháng 6 2018
Gọi số có hai chữ số đó là \(\overline{ab}\). \(\left(0\le b\le9,0< a\le9,a;b\in N\right)\)
Khi viết thêm 1 chữ số 0 xen giữa hai chữ số của nó, ta được số: \(\overline{a0b}\)
Theo bài ra, ta có:
\(\overline{a0b}=7.\overline{ab}\)
\(\Leftrightarrow a.100+b=7.\left(a.10+b\right)\)
\(\Leftrightarrow a.100+b=70.a+7.b\)
\(\Rightarrow a.30=b.6\)
\(\Leftrightarrow5.a=b\)
Do\(b< 10\Rightarrow a< 10:5=2\)
Mà \(a>0\Rightarrow a=1\)
Thay \(a=1\)vào, ta được:
\(1.5=5=b\)
\(\Rightarrow\overline{ab}=15\)
Vậy số có hai chữ số đó là \(15.\)
V
7 tháng 7 2019
gọi số có 2 chữ số cần tìm là ab(a,b là số; a khác 0 )
khi viết thêm chữ số 0 vào giữa số đó ta được số mới là a0b
khi đó theo bài ra ta có:
a0b = 7 x ab
\(\Rightarrow\)a x 100 + b = 7 x(a x 10 + b)
\(\Rightarrow\)a x 100 + b = a x 70 + b x 7
\(\Rightarrow\)a x 100 - a x 70 = b x 7 - b
\(\Rightarrow\)a x 30 = b x 6
\(\Rightarrow\)a x 5 = b
\(\Rightarrow\)a = 1( vì b là số và a khác 0)
\(\Rightarrow\)b = 5
vậy số phải tìm là 15
Có 3 số nguyên tố và 3 hợp số
=> a = b = 3
=> 6a+9b = 6a+9a = 15a = 15 . 3 = 45