Cho ABC nội tiếp đường tròn O, các đường cao AD,BE,CF. AD cắt (O) tại K. CMinh HD=HK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK
26 tháng 6 2021
a) Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BCEF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm I của đường tròn ngoại tiếp tứ giác BCEF là trung điểm của BC
AT
28 tháng 6 2021
bạn tham khảo ở đây nha,bài này mình từng làm rồi
https://hoc24.vn/cau-hoi/881cho-tam-giac-abc-nhon-noi-tiep-duong-tron-o-cac-duong-cao-adbecf-cat-nhau-tai-ha-chung-minh-tu-giac-bcef-noi-tiep-va-xac-dinh-tam-i-cua-duong-tron-ngoai-tiep-tu-giacb-duong-thang-ef-cat-duon.1092906662181
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2022
Hai góc này không bằng nhau thì chứng minh làm sao được em?
Em thử sử dụng tính năng đo góc của geogebra là biết.
DT
4 tháng 2 2022
ta có: \(MC^2=MI.MA\)
\(\Rightarrow MD^2=MI.MA\) ( do tam giác MCD cân tại M)
\(\Rightarrow\dfrac{MD}{MA}=\dfrac{ MI}{MD}\)
Xét tam giác MDI và tam giác MAD có :
\(\left\{{}\begin{matrix}DMAgócchung\\\dfrac{MD}{MA}=\dfrac{MI}{MD}\end{matrix}\right.\)
=> tam giác MDI đồng dạng tam giác MAD ( g -c)
=> góc MDI = góc MAD (1)
tứ giác DNIC nội tiếp => góc MDI = góc MCI (2)
từ 1 và 2 suy ra :góc NCI = góc HAD
mà góc MAD = góc KCI
=> góc NCI = góc KCI
vậy 3 điểm C ; K ; N thẳng hàng ( đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2022
ACDF nội tiếp nên \(\widehat{BAC}+\widehat{CDF}=180^0\Rightarrow\widehat{BAC}=\widehat{CDN}\)
ABIC hiển nhiên nội tiếp \(\Rightarrow\widehat{BAC}+\widehat{NIC}=180^0\)
\(\Rightarrow\widehat{CDN}+\widehat{NIC}=180^0\Rightarrow CDNI\) nội tiếp
\(\Rightarrow\widehat{NDI}=\widehat{NCI}\) (cùng chắn IN)
MCD cân \(\Rightarrow MC=MD\Rightarrow MD^2=MC^2=MI.MA\Rightarrow\dfrac{MD}{MA}=\dfrac{MI}{MD}\) và \(\widehat{NMI}\) chung
\(\Rightarrow\Delta MDI\sim\Delta MAD\left(c.g.c\right)\)
\(\Rightarrow\widehat{NDI}=\widehat{MAD}\Rightarrow\widehat{MAD}=\widehat{NCI}\)
Mà \(\widehat{MAD}=\widehat{KCI}\) (cùng chắn cung IK)
\(\Rightarrow\widehat{KCI}=\widehat{NCI}\) hay K, N, C thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2022
Đây chắc là 1 câu trong 1 bài nào đó, ít nhất em cũng phải nêu những câu trước có gì để người khác đỡ phải chứng minh từ đầu chứ?
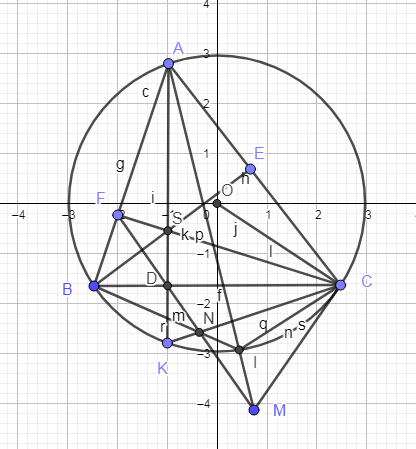
bổ sung H là trực tâm, cm HD = DK ( sửa đề )
Xét tứ giác CEFB có ^CEB = ^CFB = 900
mà 2 góc này kề, cùng nhìn cạnh BC
Vậy tg CEFB nt 1 đường tròn
=> ^EFC = ^EBC ( 2 góc nt chắn cung EC )
Xét tứ giác AFHE có
^AFH + ^AEH = 1800
mà 2 góc này đối
Vậy tg AFHE nt 1 đường tròn
=> ^HFE = ^HAE ( 2 góc nt chắn cung EH )
=> ^EAH = ^EBC
mà ^CAK = ^CBK ( 2 góc nt chắn cung CK của đường tròn O )
=> ^HBD = ^DBK
Vậy tam giác HBK cân tại B
mà BD là đường cao đồng thời là đường trung tuyến
=> HD = DK
.