tính nhanh 2016 x 2019+4038/2018 x 2020
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 8 2022
Đúng(1)
Những câu hỏi liên quan
LD
2
31 tháng 8 2017
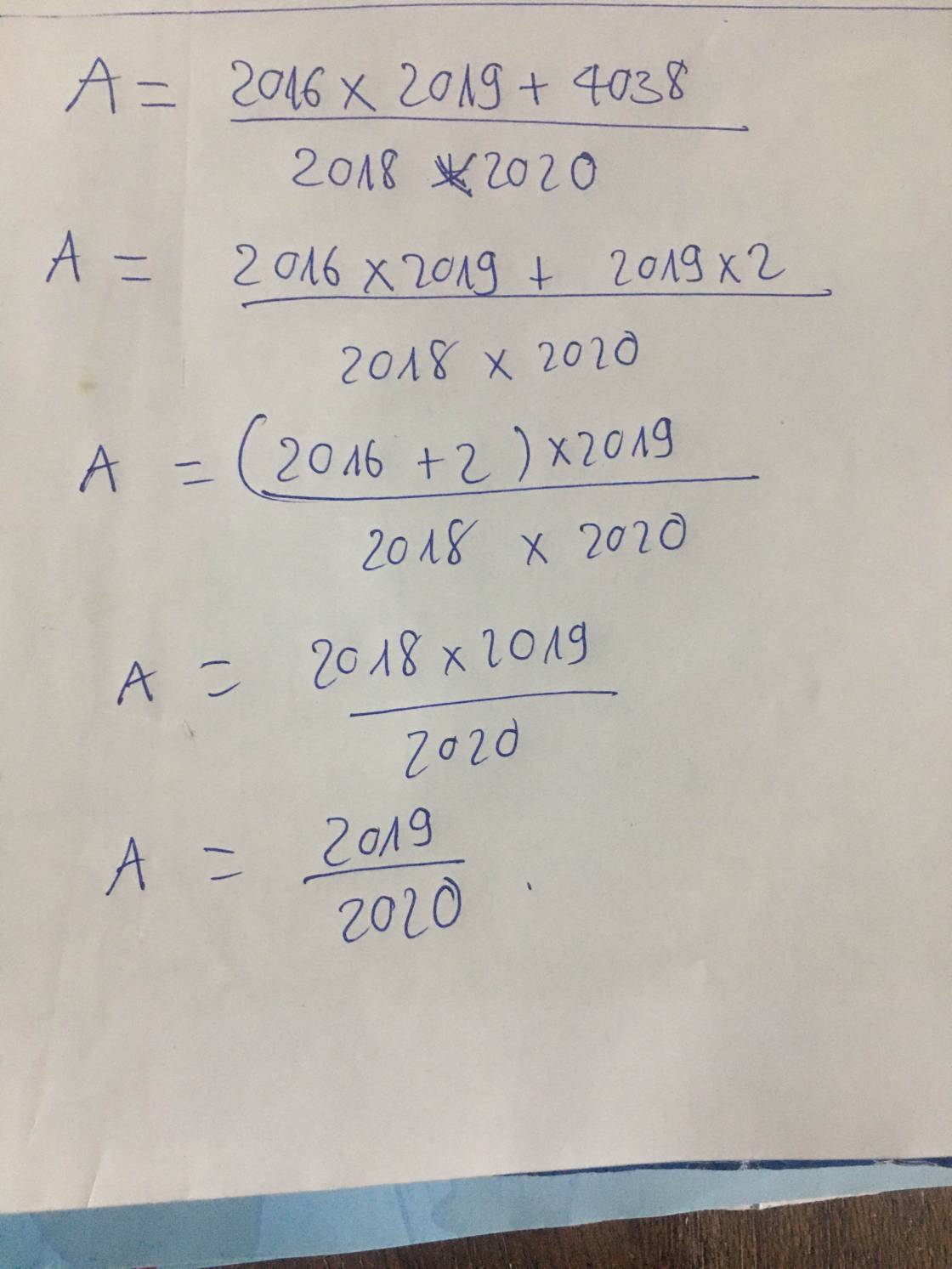
\(\frac{2016}{2017}\)x \(\frac{2017}{2018}\)x \(\frac{2019}{2020}\)=\(\frac{504}{505}\)
đ/s:\(\frac{504}{505}\)
CC
5 tháng 1 2020
\(x=2019\)\(\Rightarrow x+1=2020\)
\(\Rightarrow B=x^{2019}-\left(x+1\right).x^{2018}+........-\left(x+1\right).x^2+\left(x+1\right).x+1\)
\(=x^{2019}-x^{2019}+x^{2018}+.......-x^3-x^2+x^2+x+1\)
\(=x+1=2020\)
Vậy tại \(x=2019\)thì \(B=2020\)
TN
5 tháng 1 2020
Ta có x=2019
=> x + 1=2020
thay x+1 vào B, ta có:
\(A=x^{2019}-\left(x+1\right)x^{2018}+\left(x+1\right)x^{2017}-...+\left(x+1\right)x-1\)
=> \(A=x^{2019}-x^{2019}-x^{2018}+x^{2018}+x^{2017}-...+x^2+x-1\)
=> \(A=x-1=2020-1=2019\)
NH
23 tháng 6 2019
\(\frac{x+2019}{x+2018}=\frac{4038}{4037}\)
\(\Rightarrow\left(x+2019\right)4037=\left(x+2018\right)4038\)
\(\Rightarrow4037x+\left(4037\times2019\right)=4038x+\left(4038\times2018\right)\)
\(\Rightarrow4037x+8150703=4038x+8148684\)
\(\Rightarrow4037x-4038x=-8150703+8148684\)
\(\Rightarrow-x=-2019\)
\(\Rightarrow x=2019\)
P/s: Số to kinh -_- Ko chắc đúng đâu.
KC
2
8 tháng 2 2023
(x+2019) x 4037=(x+2018) x 4038
⇒4037�+(4037×2019)=4038�+(4038×2018)⇒4037x+(4037×2019)=4038x+(4038×2018)
⇒4037�+8150703=4038�+8148684⇒4037x+8150703=4038x+8148684
⇒4037�−4038�=−8150703+8148684⇒4037x−4038x=−8150703+8148684
⇒−�=−2019
⇒�=2019⇒x=2019
6 tháng 6 2024
x+2019) x 4037=(x+2018) x 4038
⇒4037�+(4037×2019)=4038�+(4038×2018)⇒4037x+(4037×2019)=4038x+(4038×2018)
⇒4037�+8150703=4038�+8148684⇒4037x+8150703=4038x+8148684
⇒4037�−4038�=−8150703+8148684⇒4037x−4038x=−8150703+8148684
⇒−�=−2019
⇒�=2019⇒x=2019
1 tick với nha
25 tháng 4 2023
Vì:
khi tính bài toán 2015/2016 + 2016/2017 + 2017/2018 + 2018/2019 + 2019/2020 + 2020/2015 này ra thì ta được con số là 6,000003688 con số này phải lớn hơn số 6 nên: 6,000003688 > 6
25 tháng 4 2023
Vì:khi tính bài toán 2015/2016+2016/2017+2017/2018+2018/2019+ 2019/2020+2020/2015 ta ra được là: 6,000003688 nên: 6,000003688 > 6
5 tháng 5 2018
Bài này dễ mà!
\(P\left(2019\right)=2019^3\left(a+2016\right)+2019\left(b+2017\right)+2018=2020\)
\(\Rightarrow2019^3\left(a+2016\right)+2019\left(b+2017\right)=2\)
Có: \(P\left(-2019\right)=-2019^3\left(a+2016\right)-2019\left(b+2017\right)+2018\)
\(=-\left[2019^3\left(a+2016\right)+2019\left(b+2017\right)\right]+2018\)
\(=-2+2018=2016\)
KN
8 tháng 11 2019
\(x^{2019}-2020x^{2018}+2020x^{2017}-2020x^{2016}+...+2020x-2020\)
\(=x^{2019}-2019x^{2018}-x^{2018}+2019x^{2017}+x^{2017}\)
\(-2019x^{2016}-x^{2016}+...+2019x+x-2020\)
\(=x^{2018}\left(x-2019\right)-x^{2017}\left(x-2019\right)+x^{2016}\left(x-2019\right)\)
\(+...-x\left(x-2019\right)+\left(x-2019\right)-1\)
\(=-1\)
VT
3
7 tháng 3 2020
\(\left(x-2018\right)^3+\left(x-2020\right)^3=\left(2x-4038\right)\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=0^{^{\left(1\right)}}\)
Áp dụng bđt \(a+b+c=0\Leftrightarrow a^3+b^3+c^3=3abc\)
Ta có \(\left(x-2018\right)+\left(x-2020\right)+\left(4038-2x\right)=0\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=3\left(x-2018\right)\left(x-2020\right)\left(4038-2x\right)\)
Do đó (1) \(\Leftrightarrow3\left(x-2018\right)\left(x-2020\right)\left(4038-x\right)=0\)
<=> x-2018 =0 hoặc x-2020 = 0 hoặc 4038 -2x =0
<=> x=2018 hoặc x=2020 hoặc x=2019
Vậy phương trình đã cho có nghiệm S={2018;2020;2019}
LT
7 tháng 3 2020
\(\left(x-2018\right)^3+\left(x-2020\right)^3=\left(2x-4038\right)^3\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=0\)
ta có \(\left(x-2018\right)+\left(x-2020\right)+\left(4038-2x\right)=0\)
nên đặt \(\left(x-2018\right)=a;\left(x-2020\right)=b;\left(4038-2x\right)=c\Leftrightarrow a+b+c=0\)
Khi đó a3 + b3+c3 = 0 ( 1)
mà a+b+c=0 \(\Leftrightarrow\)a+b=-c
\(\Leftrightarrow\)(a+b)3 = -c3
\(\Leftrightarrow\)a3+b3+c3 = 3abc (2)
Từ (1) và (2) \(\Leftrightarrow\)abc=0
\(\Leftrightarrow\)\(\left(x-2018\right)=0hoặc\left(x-2020\right)=0hoặc\left(4038-2x\right)=0\)
\(\Leftrightarrow\)\(x=2018hoặcx=2020hoặcx=2019\)
Vậy tập nghiệm của PT là S={2018;2019;2020}